Se realiza una descripción de los algoritmos de búsqueda aplicados en problemas tipo rejilla y grafos, con el objetivo de encontrar una ruta que conecte dos puntos dentro de un espacio de búsqueda. Se visualiza de manera gráfica el comportamiento de los algoritmos: DFS, BFS, Nayfeth y S Star. Estos algoritmos se utilizan en planificación de trayectorias y optimización de rutas en inteligencia artificial. Así mismo, se hace una representación interna del gra-fo asociado que tiene un laberinto.
Palabras clave: algoritmo de búsqueda, bfs, dfs, nayfeth, a star
A description of the search algorithms used in grid and graph type problems, with the aim of finding a path connec-ting two points in a search space is performed. DFS, BFS, Nayfeth and A Star the behavior of the algorithms is displayed graphically. These algorithms are used in path planning and route optimization in artificial intelligence. Likewise, an internal representation of the graph having associated a labyrinth is made.
Keywords: search algorithms, bfs, dfs, nayfeth, a star
La resolución de problemas en inteligencia artificial requiere, normalmente, determinar una secuencia de acciones o decisiones. Esta secuencia será ejecutada por un “explorador” con el fin de alcanzar un objetivo a partir de una situación inicial dada. Dependiendo del problema en específico, la ejecución de la secuencia de acciones o decisiones tiene asociado un costo que se tratará de minimizar, o bien tienen asociado un beneficio que se tratara de maximizar. En la descripción de los espacios de búsqueda se supondrá que el “explorador” se mueve en un entorno accesible, o que es capaz de percibir el entorno con precisión y que tanto el costo o beneficio de las acciones se pueden percibir con exactitud [11, 9, 8].
En la sección uno se realiza una descripción de conceptos de teoría de grafos y la relación que hay entre el espacio de búsqueda y grafos. En la sección dos se describen el funcionamiento de los algoritmos aplicados en problemas tipo rejilla.
Los grafos son estructuras discretas que constan de vértices y aristas que conectan estos vértices. Hay diferentes tipos de grafos que difieren en la clase y número de aristas que conectan un par de vértices. En este proyecto se introducen algunos conceptos de particular interés [7, 6, 16, 17].
Un grafo G = {V, E} está formado por un conjunto de vértices, V, y un conjunto de aristas, E. Cada arista es un par (u, v), donde u, v є V. En ocasiones los vértices se denominan nodos y las aristas arcos.
Algunas veces las aristas tienen una tercera componente, denominada peso o costo. Así, un grafo es una forma de representar conexiones o relaciones entre pares de objetos de algún conjunto V.
Las aristas en un grafo pueden ser dirigidas o no dirigidas. Se dice que una arista (u, v) es dirigida de u a v si el par (u, v) es ordenado y u precede a v. Se dice que una arista es no dirigida si el par (u, v) no es ordenado. A veces, las aristas no dirigidas se les representa con la notación de conjuntos, como por ejemplo {u, v}, pero para simplificar aquí se usa la notación (v, u) teniendo en cuenta que, en el caso no dirigido, (u, v) es lo mismo que (v, u). Los grafos suelen visualizarse trazando los vértices en forma de óvalos o rectángulos y las aristas como segmentos o curvas que unen pares de vértices.
Si todas las aristas de un grafo son no dirigidas, se dice que es un grafo no dirigido. En el caso de un grafo dirigido, llamado también dígrafo todas sus aristas son dirigidas. A un grafo que tiene aristas dirigidas y no dirigidas al mismo tiempo se le llama también grafo mezclado.
Ejemplo: Se puede modelar una ciudad con un grafo cuyos vértices son los cruceros o las calles cerradas, y cuyas aristas son tramos de calles sin cruceros. Este grafo tiene aristas no dirigidas, que corresponden a calles con doble circulación, así como aristas dirigidas que corresponden a calles con un sentido de circulación. De esta forma, el grafo que modela un mapa de ciudad es un grafo mezclado.
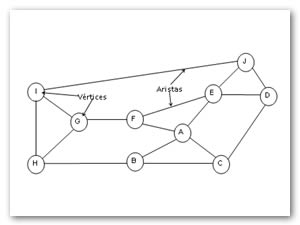
Figura 1 Símbología de un grafo.
Se dice que dos vértices son adyacentes uno con otro si están conectados por una arista. Así en la figura 1, los vértices I y G son adyacentes, pero los vértices I y F no lo son. Los vértices adyacentes de un vértice a veces se les llaman vecinos. Por ejemplo, los vecinos de G son I, H y F.
Un camino en un grafo es una secuencia de vértices w1, w2,…, wn tal que (wi, wi+1) є E para 1 <= i < n. La longitud de dicho camino es el número de aristas en el camino, es decir, n-1.Esta longitud se denomina longitud del camino sin pesos. La longitud del camino con pesos es la suma de los costos o pesos de las aristas en el camino.
La Figura 1 muestra un camino del vértice B al vértice J que pasa a través de los vértices A y E. Podemos llamar este camino B, A, E, J. Puede existir más de un camino entre dos vértices; otro camino de B a J es B, C, D, J.
Un grafo es conectado si hay al menos un camino desde cualquier vértice a otro vértice cualquiera. Sin embargo, si no existe un camino entre todos los vértices, se dice que es un grafo no conectado.
Como se define en teoría de grafos, un laberinto presenta una colección finita de callejones adjuntos (corredores) de diferentes maneras con intersecciones claramente definidas [2]. Un laberinto puede ser representado por un grafo, donde los pasillos del laberinto son las aristas y sus intersecciones los vértices del grafo, Figura 2.
Supóngase que se conoce la ubicación actual y el punto a donde se desea llegar (objetivo). Por ejemplo, considere un camino (llamado línea principal o línea R), el cual representa la línea que conecta los puntos iniciales S y T. Si no existen obstáculos en la línea R, se podría ir directamente de S a T. De otra manera, se tiene que maniobrar usando algún algoritmo u otro para poder llegar al objetivo [13]
Un buen algoritmo debería combinar el razonamiento, ejecución y capacidad “humana” para resolver laberintos pequeños. Algunos algoritmos tienen gran capacidad para encontrar caminos en un laberinto, otros, pueden producir caminos cortos en un laberinto pequeño, pero caminos muy largos para laberintos mas complejos, forzando a visitar el mismo segmento (callejón) de un laberinto varias veces.
La representación de una laberinto por medio de un grafo, brinda la posibilidad de analizar sólo la estructura del grafo; para aplicar la teoría de grafos, es necesario hacer o conocer la estructura del grafo e incluso tomar en cuenta ciertas propiedades para poder decidir que algoritmos son los más adecuados para su implementación.
La figura 2 a) muestra un laberinto con su correspondiente grafo interno, en la figura 2 b) se asigna a cada vértice la posición fila-columna [i, j] dentro del laberinto.
Figura 2. Grafos y laberintos: a) Representación grafo interno de un laberinto, b) Grafo ramificado, representa conexión de las posiciones [i, j].
La ventaja de asociar un laberinto como un grafo, permite aplicar recorrido de grafos para encontrar la conexión entre dos nodos, entre los algoritmos que se pueden aplicar están: primera búsqueda en amplitud, primera búsqueda en profundidad, Dikjstra y S Star.
La búsqueda de una ruta entre dos nodos considera la posibilidad de encontrar un camino que conecte los dos vértices, en ocasiones, el propósito también es encontrar la ruta más corta convirtiendo el problema en un caso de optimización, de tal manera que sea posible encontrar la ruta con el menor costo posible entre dos puntos dados. Entre los algoritmos que se encuentran en la literatura están: Depth First Search (DFS), Breadth First Search (BFS), A Star y Dijkstra [3, 4, 5, 7, 11], este último permite agregar pesos en las aristas del grafo para ejemplificar el costo que implica ir de un vértice a otro. Sin embargo, en este apartado, se ejemplificará el funcionamiento de estos algoritmos en espacios de búsqueda tipo rejilla [8, 1]. Debido a que en laberinto se puede modelar también como un arreglo bidimensional de N x M, en la que hay celdas libres y celdas pared. Un laberinto es un área de dos dimensiones en forma de rejilla de cualquier tamaño, por lo general rectangular. El laberinto se compone de celdas. Una celda es un elemento del laberinto, limitado formalmente espacio. El laberinto puede contener diferentes obstáculos en cualquier cantidad [1].
El algoritmo de búsqueda en amplitud, etiqueta todas las celdas (habitaciones), buscando la celda de final en todos sus vecinos adyacentes. Si no se llega a la celda “T”, la búsqueda continua hacia habitaciones adyacentes encontradas a partir de la habitación inicial; hasta que la celda “T” sea localizada. El algoritmo debe mantener la “ruta” de las habitaciones visitadas y que celdas son vecinos inmediatos desde la celda inicial, etiquetando cada celda con un número cada vez mayor a la celda por la que llegó [2, 12, 14].
Pasos:
Los resultados del algoritmo se muestran en la Figura 4.
Este algoritmo etiqueta todas las habitaciones como no visitadas, usa una pila para recordar donde debe ir cuando alcanza un extremo muerto (callejón sin salida) [16, 17].
Elija una habitación inicial “S” y final “T”.
Regla 1: Si es posible, visitar una habitación (si hay más de una, se elige al azar) adyacente no visitado, marcarlo como visitado, si la celda actual es la objetivo, terminar.
Regla 2: Si no se puede aplicar la regla 1, entonces, si es posible, regresar a la ultima bifurcación (parte del laberinto donde se tiene más de dos “caminos”).
Regla 3: Si no se puede aplicar la regla 1 o regla 2, el proceso ha terminado.
Este algoritmo encuentra un camino si es que existe, y se puede aplicar a laberintos de conexión simple o múltiple (tienen circuitos internos), pero no garantiza dar la ruta más corta. La Figura 3, ejemplifica el procedimiento.
Figura 3. Primera búsqueda en profundidad.
Figura 4. Búsqueda en amplitud.
Un laberinto se puede representar como un arreglo bidimensional con valores “1” y “0” representando paredes y pasillos (celdas libres) respectivamente [2,10]. Cada celda tiene vecinos adyacentes en cuatro direcciones: Norte, Sur, Este y Oeste.
Este algoritmo se basa en las siguientes reglas.
Se elige una celda inicial E y final S, ambas celdas tienen “0”, estas deben ser distintas, Figura 5 a).
Figura 5. Laberinto inicial. b) Resultado después de aplicar el algoritmo de Nayfeth.
Al aplicar las reglas, el algoritmo bloquea todos los puntos muertos (callejones sin salida) en el laberinto. Cada celda libre es accesible solamente en una dirección (i.e. Tres celdas pared alrededor de una celda, debe ser un callejón sin salida y por consiguiente no puede ser parte de la solución). Las celdas libres se hacen nuevas celdas pared, y este procedimiento se repite hasta que el “espacio de búsqueda” queda sin cambios. Cuando no hay cambios, las únicas celdas libres son la solución del laberinto, Figura 5 b).
Suponga que se tiene el laberinto de la Figura 6 a). Es un laberinto de conexión múltiple, hay más de un camino desde el punto de entrada al de salida. También, tiene un circuito interno. Este algoritmo no funciona adecuadamente para este tipo de laberintos. En este caso, es recomendable aplicar primero el algoritmo de Nayfeth después el de BFS.
Figura 6. a) Laberinto inicial con dos soluciones posibles. b) Resultado algoritmo de Nayfeth. c) Resultado con el algoritmo de BFS.
Este algoritmo utiliza una búsqueda heurística para encontrar la ruta óptima entre dos puntos. Maneja tres funciones: F, G y H.
En la figura 7, se utiliza un entorno en la que se representan movimientos horizontal, vertical y diagonal, en la que éste último genera un costo más alto que los dos primeros. Para este caso en particular, se asigna un costo de 10 unidades para movimientos en horizontal o vertical y un costo de 14 unidades para movimientos en diagonal. En la figura 7, la celda E representa el punto de partida, la celda S el punto objetivo o meta, las celdas libres representan color blanco y las celdas de color negro representan los obstáculos en el espacio de búsqueda.
Figura 7 Trayectoria óptima que enlaza la entrada y la salida del laberinto utilizando A*.
El costo de la función H, se calcula con una distancia de Manhattan, que consiste en sumar la cantidad de bloques en horizontal y vertical que restan para llegar a la meta y multiplicar por el costo que tiene asignado este tipo de movimientos. Para mayor detalle del algoritmo A estrella se puede consultar [11, 18].
Los algoritmos de búsqueda de rutas DFS y BFS permiten encontrar la celda objetivo en espacios de búsqueda en la que se desconoce la celda objetivo, sin embargo, hay ocasiones en las que en el proceso de encontrar la celda objetivo, estos recorren gran parte de espacio de búsqueda.
El algoritmo de Nayfeth realiza una discriminación de las celdas libres, convirtiendo estas en celdas pared, pero combinado con el BFS ofrece buenos resultados. Se aplica en espacios con objetivo desconocido.
El algoritmo A estrella permite hacer movimientos en diagonal, horizontal y vertical, lo que reduce la longitud del camino encontrado debido a que se conoce de manera previa el punto a donde se desea, llegar es decir, es conocido, utiliza una heurística, lo que marca una tendencia hacia la meta reduciendo de manera significativa el espacio de búsqueda. Este algoritmo es uno de los más aplicados debido a que encuentra la solución óptima entre dos puntos siempre y cuando estén conectados.
[1] A.J. Bagnall, Z.V. Zatuchna, “On the Classification of Maze Problems,” Applications of Learning Classifier Systems, Studies in, Bull, Springer, pp. 307-316, 2005.
[2] Tomas M. V.T. “Generación y ampliación de Laberintos”, Tesis de maestría, CITIS-UAEH, Pachuca de Soto, Hidalgo, México, Diciembre 2007.
[3] Dijkstra E. W., “A Note on Two Problems in Connexion with Graphs”, Numerische Mathematik, Vol. 1, pp. 269-271, 1959.
[4] Even S., “Chapter 3: Depth-First Search”, Technion Israel Institute of Technology January 1, 2003.
[5] Goodrich M. T. and Tamassia R. “Data Structures and Algorithms in Java”, Fourth Edition. John Wiley & Sons, Inc., Section 13.7.1: Kruskal's Algorithm, pp.632, 2006.
[6] Harell D., “Graph Drawing by High-Dimensional Embedding”, Journal of Graph Algorithms and Applications, http://jgaa.info/ vol. 8, no. 2, pp. 195–214 (2004).
[7] Johonsonbaugh R., “Matemáticas Discretas”, Prentice Hall, 6ta. Edición, 2005.
[8] Molina V. J., Torres P. C., Restrepo P. C., “Técnicas de inteligencia artificial para la solución de laberintos de estructura desconocida”, Scientia et Technica Año XIV, No 39, Universidad Tecnologica de Pereira, ISSN: 012221701, 2008.
[9] Moore E. F., “The Shortest Path Through a Maze”, Annals of Computation Laboratory of Harvard University, Harvard University Press, vol. 30, pp. 285-292,1959.
[10] Nayfeth B., “Cellular Automata for Solving Mazes”, Doctor Dobb’s Journal, February 1993.
[11] Palma M. y Roque M. Morales, “Inteligencia Artificial: Técnicas, métodos y aplicaciones”, Mc Graw Hill, 2008, capítulo 8.
[12] Rubin F., “The Lee Path Connection Algorithm”, IEEE, Vol. c-23, No. 9, September 1974.
[13] Sedgewick R., “Algorithms (Third edition) in Java Parts Graph Algorithms With Java”, consulting by Machael Schildlowsky, 2003.
[14] Sheldon A. B., “A Modification of Lee’s Algorithm”, IEEE, Transactions on Electronic Computers, Febrero, 1967.
[15] Tamassia M. T. y Goodrich R.,”Estructura de Datos y Algoritmos en JAVA”, 2da. Edición., CECSA, 2002.
[16] Waite M. and Lafore R., “Data Structures & Algorithms in JAVA”, Signature Series, 1998
[17] Weiss M. A., “Estructura de Datos en JAVA”, compatible con JAVA 2, Pearson Addison Wesley, 2000.
[18] http://www.policyalmanac.org/games/articulo1.htm. Consulta: 14/01/2014
[a] 1Universidad Autónoma del Estado de Hidalgo: Escuela Superior de Huejutla.
Huejutla de Reyes, Hidalgo, México, C.P. 43000
{victor_tomasm, felipe.huejutla,efra_a_h}@hotmail.com