Código de borrado
Resumen
El código de borrado es un método para la protección de datos en el que los datos se dividen en fragmentos redundantes que se expanden y codifican, y se almacenan en diferentes ubicaciones, como pueden ser discos o nodos de almacenamiento, esto para permitir que los datos que son alterados o dañados se puedan reconstruir mediante el uso de información sobre los datos almacenados en otra parte de la matriz o incluso en una ubicación geográfica diferente.
Palabras clave: Código de borrado, protección de datos
Abstract
The erasure code (Erasure Code or EC) is a method for data protection in which the data is divided into redundant fragments that are expanded and encoded, and stored in different locations, such as disks or storage nodes, this is to allow data that is altered or damaged to be reconstructed by using information about data stored elsewhere in the array or even in a different geographical location.
Keywords: Erasure code, data protection
Introducción
Los códigos de borrado utilizan una función matemática para describir una serie de números, de modo que puedan ser comprobados por su exactitud y recuperarlos si uno está perdido. La protección que ofrece el código de borrado se representa mediante la siguiente ecuación n= k + m. La variable “k” representa la cantidad original de datos, la variable “m” corresponde a los datos adicionales o redundantes que se añaden para proporcionar protección contra fallas, la variable “n” es el número total de datos creados después del proceso de codificación.
Los códigos de borrado fueron desarrollados hace más de 50 años y varios han sido los tipos de código de borrado que han surgido.
Los códigos de borrado pueden ser útiles con grandes cantidades de datos y cualquier aplicación o sistema que necesita tolerar fallas, como lo son las redes de datos, aplicaciones de almacenamiento distribuido, almacenes de objetos y archivos. Un caso actual para la codificación de borrado es el almacenamiento en la nube basada en objetos. [1]
Desarrollo
En el presente documento se habla sobre los diferentes tipos de código de borrado que existen, y las implementaciones que estos tienen, ya que mucho depende de las ventajas que este ofrezca a quien desea un almacenamiento seguro de sus datos, uno de los que mencionaremos y que a su vez es uno de los más comunes, es el de reed-solomon, este puede ser utilizado para la corrección de errores de fallos múltiples en los sistemas que son similares a RAID, por otro lado están los sistemas más utilizados, anteriores a los código de borrado que si bien se utilizan para el mismo fin, estos son los sistemas RAID los cuales permiten que los mismos datos se almacenen en diferentes lugares en múltiples discos duros y ayuda a proteger contra las fallas de la unidad, a continuación, se mencionan algunos:
- Código Reed-Solomon (RS)
Los códigos de Reed-Solomon, tiene la historia más larga. La unidad de tira es una palabra w- bit, donde w debe ser lo suficientemente grande como para que n ≤ + 1. Para que las palabras puedan ser manipuladas eficientemente, w es típicamente restringido para que las palabras caigan en los límites de la máquina: w ∈ {8,16,32,64}. Sin embargo, siempre que n ≤ + 1, el valor de w se puede elegir a discreción del usuario. La mayoría de las implementaciones eligen w=8, ya que sus sistemas contienen menos de 256 discos, yw = 8. Los códigos de Reed – Solomon tratan cada palabra como un número entre 0 y – 1, y operan en estos números con la aritmética de Campo de Galois (D()), que define adición, multiplicación y división en estas palabras de tal manera que el sistema es cerrado y bien comportado.
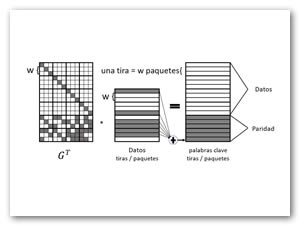
El acto de codificar con códigos Reed – Solomon es álgebra lineal simple. Una matriz generadora se construye a partir de una matriz de Vandermonde, y esta matriz se multiplica por las k palabras de datos para crear una palabra de código compuesta por los k datos y las palabras de codificación m. dicho proceso se representa en la siguiente figura 1.
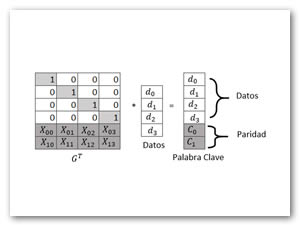
Ilustración 1 Reed – Solomon que codifica para k = 4 y m = 2. Cada elemento es un número entre 0 y 2^w – 1 Realización propia
Cuando los discos fallan, uno decodifica borrando filas de , invirtiéndolo y multiplicando el inverso por palabras que sobreviven. Este proceso es equivalente a resolver un conjunto de ecuaciones lineales independientes. La construcción de a partir de la matriz de Vandermonde asegura que la inversión de la matriz siempre tiene éxito.
En (), la adición es equivalente a bit – exclusivos – o (XOR), y la multiplicación es más compleja, típicamente implementado con tablas de multiplicación o tablas de logaritmos discretos. Por esta razón, los códigos de Reed – Solomon se consideran costosos. Existen varias implementaciones open – source de la codificación RS. [2]
- Códigos Cauchy Reed – Solomon (CRS)
Los códigos CRS modifican los códigos RS de dos maneras. En primer lugar, emplean una construcción diferente de la matriz generando y usando matrices de Cauchy en lugar de matrices de Vandermonde. En segundo lugar, eliminan las costosas multiplicaciones de códigos RS al convertirlas en operaciones extra XOR. Tenga en cuenta que esta segunda modificación también puede aplicarse a los códigos RS basados en Vandermonde. Esta modificación transforma de una matriz de palabras w- bit a una matriz de bits. Al igual que con la codificación RS, w debe seleccionarse de modo que n ≤ + 1.
En lugar de operar en palabras simples, la codificación CRS opera en tiras enteras. En particular, las tiras se dividen en w paquetes, y estos paquetes pueden ser grandes. El acto de codificación ahora sólo implica operaciones XOR – un paquete de codificación se construye como la XOR de todos los paquetes de datos que tienen un bit en la fila del paquete de codificación de .
Dicho proceso se representa en la figura 2, el cual se ilustra cómo se crea el último paquete de codificaciones como el XOR de los seis paquetes de datos identificados por la fila de .
Para que los XOR sean eficientes, el tamaño del paquete debe ser un múltiplo del tamaño de la palabra de la máquina. Por lo tanto, el tamaño de la tira es igual a w veces el tamaño del paquete. Puesto que w ya no se relaciona con los tamaños de palabras de máquina, w no está restringido a [8, 16, 32, 64]; en su lugar, cualquier valor de w puede ser seleccionado siempre y cuando n ≤ .
La decodificación en CRS es análoga a la codificación RS, todas las filas de que corresponden a paquetes fallidos se eliminan, y la matriz se invierte y se emplea para recalcular los datos perdidos.
Dado que el rendimiento de la codificación CRS está directamente relacionado con el número de los en , se ha realizado una investigación sobre la construcción de matrices de Cauchy que tienen menos que las construcciones originales CRS. La biblioteca Jerasure utiliza transformaciones matrices adicionales para mejorar aún más estas matrices. Además, en el caso restringido cuando m=2, la biblioteca de Jerasure utiliza resultados de una enumeración previa de todas las matrices de Cauchy para emplear matrices probablemente óptimas para todo w ≤ 32. [2]
- EVENODD Y RDP
Son dos códigos desarrollados para el caso especial de RAID – 6, que es cuando m=2. Convencionalmente en RAID – 6, la primera unidad de paridad está etiquetado P, y el segundo está marcado como Q. la unidad P es equivalente a la unidad de paridad en un sistema RAID – 4, y la unidad Q está definida por ecuaciones de paridad que tienen patrones distintos.
Aunque sus especificaciones originales utilizan términos diferentes, EVENODD y RDP encajan en el mismo paradigma que la codificación CRS, con tiras compuestas de paquetes w. En EVENODD, w es constreñido tal que es un número primo. En RDP, debe ser primo y . Ambos códigos funcionan mejor cuando () se minimiza. En particular, RDP logra un rendimiento óptimo de codificación y decodificación () operaciones XOR por palabra de codificación cuando k=w o . El rendimiento de ambos códigos disminuye a medida que () aumenta. [2]
- Códigos de RAID – 6 de densidad mínima
Si codificamos usando una matriz de bits generando para RAID – 6, la matriz es bastante limitada. En particular, las primeras filas de componen una matriz de identidad, y para que la unidad P sea paridad recta, las siguientes filas w deben contener k matrices de identidad. La única flexibilidad en una especificación RAID – 6 es la composición de los últimos w filas. En, Blaum y Roth demuestran que cuando , estas w filas restantes deben tener al menos para que el código sea MDS. Se denominan matrices MDS que alcanzan este límite inferior Densidad Mínima de Códigos.
Existen tres construcciones diferentes de códigos de Densidad Mínima para diferentes valores de w:
- Blaum – Roth codifica cuando es primo.
- Códigos de liberación cuando w es primo.
- El código de liberación cuando w = 8.
Estos códigos comparten las mismas características de rendimiento. Codifican con operaciones XOR por palabra de codificación. Por lo tanto, se desempeñan mejor cuando w es grande, logrando óptima asintótica como . Su desempeño de decodificación es ligeramente peor, y requiere una técnica llamada Reconstrucción hibrida especifica de código para lograr un rendimiento casi óptimo.
Los códigos de Densidad Mínima también logran un rendimiento de actualización casi óptimo cuando se modifican piezas individuales de datos. Este rendimiento es significativamente mejor que EVENODD y RDP, que son peores por un factor de aproximadamente 1,5. [2]
- Optimización RAID – 6 de Anvin
En 2007, Anvin publicó una optimización de las codificaciones RS para RAID – 6. Para esta optimización, la fila de correspondiente a la unidad P, contiene todas las unidades, de manera que la unidad P puede ser paridad. La fila correspondiente a la unidad Q contiene el número 2 en GF () en la columna (iniciada en cero) de manera que el contenido de la unidad Q puede calcularse sucesivamente XOR -ing los datos de la unidad en la Q multiplicar esa suma por dos. Dado que la multiplicación por dos se puede implementar mucho más rápido que la multiplicación general en GF (), esto optimiza el rendimiento de la codificación sobre las implementaciones RS estándar. La decodificación permanece sin optimizar. [2]
- RAID 0 (disk striping):
Características: El disco despliega los datos a través de dos o más unidades de disco con el fin de mejorar el rendimiento de I/O realizando I/O paralelos. Una enésima parte de los datos se encuentra en cada una de las unidades de disco. Siendo “n” el número de discos. La cantidad total de almacenamiento es la suma de la capacidad de todos los dispositivos del grupo.
Aplicaciones: Proporciona alto rendimiento para lecturas y escrituras. Sin embargo, no hay redundancia de datos. La RAID 0 por si sola únicamente se debería utilizar para aplicaciones que puedan tolerar perdidas de acceso a datos que se pueden obtener desde otras fuentes. [3]
- RAID 1 (disk mirroring):
Características: Los discos en espejo proporcionan protección de datos y un rendimiento de lectura mejorado. La RAID 1 duplica los datos a través de dos o más discos, de forma que los discos son idénticos entre sí. La RAID 1 utiliza la protección n+n multiplicando por dos el número de dispositivos necesarios. Ofrece un 100% de redundancia.
Aplicaciones: OLTP de lectura intensiva y otros datos transaccionales para el alto rendimiento y alta disponibilidad. [3]
- RAID 0+1:
Características: La distribución y la duplicación de los datos para proporcionar alto rendimiento (distribución) y disponibilidad (duplicación) usando un número de dispositivos n+n. La pérdida de una unidad de disco no afecta al rendimiento o a la disponibilidad, como sería el caso de la RAID 0 mientras que la distribución del disco mejora el rendimiento.
Aplicaciones: Las aplicaciones OLTP y las intensivas en I/O que requieren alto rendimiento y alta disponibilidad. Esto incluye los registros de transacción, los ficheros del diario y los índices de datos donde el cálculo de costos se basa en dólares por I/O, en comparación con dólares por unidad de almacenamiento. [3]
- RAID 1+0 (RAID 10):
Características: Parecido al RAID 0+1, duplica y distribuye datos para proporcionar alto rendimiento (distribución) y alta disponibilidad (duplicación) usando un número de dispositivos n+n. La diferencia reside en distribuir grupos de discos juntos y después duplicar los grupos de distribución.
Aplicaciones: Las aplicaciones OLTP y las intensivas en I/O que requieren alto rendimiento y alta disponibilidad. Esto incluye los registros de transacción, los ficheros del diario y los índices de datos donde el cálculo de costos se basa en dólares por I/O, en comparación con dólares por unidad de almacenamiento. [3]
- RAID 2:
Características: Divide los datos a nivel de bits distribuyéndolos entre los dispositivos del arreglo, hace uso de código Hamming para chequeo de paridad así también la segmentación a nivel de bits crea un alto impacto (lectura/escritura) en los recursos del sistema lo que lo hace inviable a nivel práctico. [4]
- RAID 3 (byte striping):
Características: Distribuye con paridad dedicada a nivel de byte y tiene una única de disco dedicada que almacena la información de paridad usando un método de n+1 en términos del número de dispositivos necesarios.
Aplicaciones: Esto proporciona un buen rendimiento para imágenes de video, geofísica, ciencias naturales u otras aplicaciones de procesamiento secuencial. La RAID 3, sin embargo, no se adapta bien a las aplicaciones que requieren operaciones simultaneas de entrada/salida de múltiples usuarios o de flujos de entrada/salida. [3]
- RAID 4 (block striping & dedicated parity):
Características: Igual que la RAID 3, pero con protección de paridad a nivel de bloques, segmenta los datos distribuyéndolos entre los dispositivos del arreglo. Dedica por completo uno de los dispositivos del arreglo para paridad. Es un esquema similar a RAID 2 y RAID 3 pero la división en bloques evita un alto impacto (lectura/escritura) en los recursos del sistema.
Aplicaciones: La utilización de la cache de lectura y escritura funciona bien con los entornos de ficheros. [3]
- RAID 5 (block striping & distributed parity):
Características: La distribución de discos y la protección de paridad rotativa usando un numero n+1 de componentes proporcionan una buena disponibilidad con un buen rendimiento para múltiples usuarios similares y flujos de entrada/salida. Mediante la utilización de una unidad de disco conectable en caliente, los datos se pueden reconstruir (reconstrucción de la unidad) para protegerse de un segundo fallo una vez completado. [3]
Segmenta los datos a nivel de bloques distribuyéndolos entre los dispositivos del arreglo de forma similar a RAID 4. RAID 4 y RAID 5 proveen redundancia ante la falla de un dispositivo en base a la información de paridad. [4]
Aplicaciones: Reduce el número de componentes requeridos mientras que proporciona una buena disponibilidad, un buen rendimiento para lecturas, el rendimiento de las escrituras se ve afectado si no se utiliza la cache de escritura. Entre las aplicaciones adecuadas para la RAID 5 se encuentran los datos de referencia, las tablas de bases de datos intensivas en lecturas, la compartición de ficheros generales y las aplicaciones web. [3]
- RAID 6 (block striping & distributed parity):
Características: La distribución del disco con paridad rotativa usando unidades de doble paridad destinadas a reducir el riesgo de disponibilidad de datos durante una reconstrucción de la unidad de disco, concretamente cuando se utilizan unidades de disco SATA y de canal de fibra de más capacidad. El problema con la RAID 6 y con cualquier esquema de paridad de múltiples unidades es la sobrecarga del rendimiento al hacer cálculos de paridad cuando se escriben datos o se reconstruye a partir de una unidad de disco que ha fallado.
Aplicaciones: Almacenamiento de grandes cantidades de datos en las que se puedan llevar a cabo reconstrucciones en segundo plano. [3]
- Niveles de RAID
| NIVEL | TASA DE FALLAS (fail rate) | POSIBLES APLICACIONES |
| RAID 0 | 1-(1-r) N | Almacenamiento de archivos grandes que no requieren redundancia en tiempo real. |
| RAID 1 | rN | Base de datos y archivos de contenido dinámico (poca capacidad). |
| RAID 4 | N(N-1)r2 | Bases de datos, servidores de archivos, correo electrónico, contenido. |
| RAID 5 | N(N-1)r2 | Bases de datos, servidores de archivos, correo electrónico, contenido. |
| RAID 6 | N(N-1)(N-2)r3 | Bases de datos, servidores de archivos, correo electrónico, contenido (mayor tolerancia a fallas que RAID 5). |
Tabla 1 Niveles de RAID Realización propia
Conclusión
Las copias de seguridad, los sistemas RAID, las redes de datos, por mencionar algunos, son sistemas obsoletos para aquellos quienes desean mayor seguridad en el almacenamiento de datos, esto se debe a que actualmente están siendo reemplazados por los códigos de borrado, y estos pueden soportar grandes cantidades de datos sin ningún problema a diferencia de los mencionados anteriormente, que si soportan una cierta cantidad de datos pero tienden a presentar mayor probabilidad de fallos, sin embargo con los códigos de borrado se tiene una mayor tolerancia a fallos, como lo definimos al iniciar el documento, en los códigos de borrado actúan de forma que cuando un dato se pierde este se recupera con la información contenida en otra ubicación, esto hace que sea uno de los que presenta mayor fiabilidad al usuario quien desea que sus datos estén más seguros, mientras que su competencia dependerá de los gastos en tecnología que inviertan para poder solucionar las fallas en sus sistemas de almacenamiento.
Referencias
[1] ComputerWeekly.com. (04 de 2014). Obtenido de http://www.computerweekly.com/feature/Erasure-coding-versus-RAID-as-a-data-protection-method
[2] Plank, J. S. (01 de 10 de 2017). Una Evaluación de Desempeño y Examen de Open-Source Erasure. Tennessee, EE. UU.
[3] TechTarget. (06 de 2007). Obtenido de http://searchdatacenter.techtarget.com/es/consejo/Definicion-de-los-niveles-de-RAID
[4] Universidad Tecnológica de Panamá. (16 de 10 de 12). Sistemas RAID. Ciudad de Panamá, República de Panamá.
[a] Alumno de la Licenciatura en Ciencias Computacionales-Escuela Superior de Huejutla eduard030696@gmail.com
[b] Alumno de la Licenciatura en Ciencias Computacionales-Escuela Superior de Huejutla alaguerrero96@gmail.com
[c] Docente de la Universidad Autónoma del Estado de Hidalgo- Escuela Superior de Huejutla raul_palacios@uaeh.edu.mx
[d] Docente de la Universidad Autónoma del Estado de Hidalgo- Escuela Superior de Huejutla felipe_nunez@uaeh.edu.mx