Applying petri nets to discrete event systems modeling
Palabras clave: Redes de Petri, Modelación, Simulación, Sistemas de eventos discretos.
Keywords: Petri nets, Modeling, Simulation, Discrete event systems.
Todo lo que nos rodea son sistemas, los cuales se han clasificado como Sistemas de Eventos Continuos y Sistemas de Eventos Discretos. Mientras que un sistema continuo es aquel que va cambiando al paso del tiempo de forma constante, un sistema discreto es aquel que cambia su estado en intervalos de tiempo variados y no de forma constante. Ejemplos de sistemas continuos son el cambio en la temperatura, la velocidad a la que cae un objeto, o el contenido de agua en un tinaco que está siendo llenado por medio de la tubería y a la vez vaciado por el uso doméstico de una casa. Por otro lado, ejemplos de sistemas discretos son; la cantidad de personas que existe en la fila de un banco, el número de vehículos esperando en una caseta de cobro, o la cantidad de productos que existen en un almacén. Como puede observarse, en los ejemplos de los sistemas de eventos discretos el valor de sus variables cambia en momentos del tiempo no necesariamente constantes; en particular, la cantidad de personas que están en un banco puede ir en aumento conforme los clientes llegan, pero va a haber lapsos de tiempo en que se mantiene la misma cantidad sin sufrir cambio alguno, en otro instante en el tiempo la cantidad de personas disminuirá, mientras que en otros aumentará.
La importancia de estudiar estos sistemas radica en conocer el tamaño de las instalaciones o velocidad en los servicios que se ofrecen en tales sistemas, para poder dar atención a los clientes o usuarios en tiempos adecuados.
Actualmente existe en el mercado una gran variedad de software aplicado a la modelación y simulación de sistemas de eventos discretos tales como ProModel®[1], Arena®[2], Flexim®[3], entre otros, que permiten contar con información estadística correspondiente al comportamiento del sistema. Los resultados obtenidos de un modelo de simulación son utilizados para realizar mejoras en el sistema modelado, ya que a partir del mismo modelo, se pueden ejecutar diferentes escenarios del modelo, con modificaciones que pudieran mejorar su funcionamiento, y tomar la decisión de modificar el sistema real o mantenerlo.
Una de las herramientas utilizadas en la modelación, simulación y análisis de Sistemas de Eventos Discretos son las redes de Petri (RdP), las cuales tienen la fortaleza de poder representar gráfica y matemáticamente un modelo para un sistema de evento discreto.
Las RdP fueron introducidas en 1962 por Carl Adam Petri, en su trabajo de tesis doctoral titulado “Kommunikation mit Automaten”, sometido en la Facultad de Matemáticas de la Universidad de Bonn, en Alemania [4]. Las RdP son una herramienta de modelación gráfica y matemática que puede aplicarse en el estudio de muchos sistemas. Con RdP se puede modelar y estudiar sistemas concurrentes, asíncronos, distribuidos, paralelos, no deterministas y/o estocásticos. Como una herramienta gráfica, las RdP pueden utilizarse como un apoyo de comunicación visual similar a diagramas de flujo, diagramas de bloques y redes. Además, los tokens son utilizados en estas redes para simular el comportamiento dinámico y concurrente de los sistemas.[5]
Como una herramienta matemática, es posible establecer ecuaciones de estado, ecuaciones algebraicas y algunos otros modelos matemáticos que denoten el comportamiento del sistema modelado.
Una RdP es un tipo particular de gráfica dirigida, adicionada con un estado inicial denominado marcado inicial (M0). El grafo N correspondiente a la RdP es dirigido, con peso y bipartito con dos tipos de nodos, llamados lugares y transiciones. Además, los arcos que conectan a estos elementos solamente pueden ligar elementos de tipo distinto. Gráficamente, los lugares son representados mediante círculos, y las transiciones mediante rectángulos o barras. [6]
Un marcado (estado) asigna a cada lugar un entero no negativo k. Este entero no negativo indica el número de tokens que contendrá cada lugar p para indicar el estado en que se encuentra el sistema modelado con la RdP. Gráficamente se colocan k puntos negros (tokens) en el lugar p. Un marcado es denotado por M, un vector-m donde m es el número total de lugares. El p-ésimo componente de M, denotado por M(p), es el número de tokens en el lugar p.
Habilitación y disparo de una transición. El comportamiento de muchos sistemas pueden ser descritos en términos de los estados del sistema y de sus cambios. Para simular el comportamiento dinámico de un sistema, el estado o marcado de la RdP es cambiado de acuerdo a la siguiente regla de disparo de transición[5]:
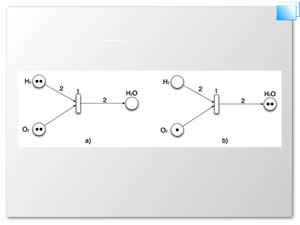
Ejemplo de una RdP y su dinámica. Para mostrar el comportamiento de un sistema modelado mediante una RdP se presenta el siguiente ejemplo tomado de [5], y se basa en la conocida reacción química del agua: 2H2 + O2--> 2H2O. En las figuras 1(a) y 1(b) se muestra la RdP que representa a la relación que existe entre las moléculas de hidrógeno (H) y de oxígeno (O) para formar moléculas de agua (H2O). Primero, en la figura 1(a), se tiene el lugar de entrada que representan la presencia de dos moléculas de H2 y el otro lugar de entrada con dos moléculas de O2. La transición t está habilitada debido a que la cantidad de tokens en los lugares de entrada (H2 y O2) es igual o mayor que el valor del peso del arco que los conecta con la transición t. Dado que t está habilitada, se procede con su disparo, desplazando los tokens en la RdP como se muestra en la figura 1(b), donde se toman dos tokens de H2, uno de O2, y se colocan dos tokens en el lugar de salida H2O, de acuerdo al valor del peso del arco que lo conecta con t. Lo que representa que después del disparo de t (ocurrencia de la reacción química) se obtienen dos moléculas de H2O.
Figura 1. Ilustración de la dinámica de disparo de transiciones en la modelación de la reacción química del agua. (a) antes del disparo de la transición t. (b) después del disparo de la transición t.
Los métodos para analizar RdP pueden clasificarse en los siguientes grupos: 1) el método de árbol de cobertura, 2) la ecuación de estado, que utiliza a la matriz de incidencia, 3) la técnica de simplificación de RdP y 4) la simulación de la RdP. El primer método tiene que ver con todas las marcas alcanzables de la marca inicial. Este método se podría aplicar a todas las clases de redes, pero está limitado a redes ”pequeñas” debido a la complejidad en el incremento del espacio de estados. Por otro lado, el enfoque de ecuación de matrices y la técnica de simplificación de RdP son muy poderosos, pero en muchos casos se pueden aplicar sólo subclases especiales de RdP o en situaciones especiales. Para modelos de RdP complejos, la simulación de eventos discretos es otra de las formas con que se pueden revisar las propiedades del sistema. [7]
El árbol de cobertura. Dada una RdP, desde su marca inicial M0 , podemos obtener igual número de marcas “nuevas” como el número de transiciones que se encuentren habilitadas. Con cada marca nueva podemos alcanzar más marcas. En el árbol obtenido, los nodos representan las marcas generadas desde M0 y sus sucesores, y cada arco representa el disparo de una transición, el cual transforma una marca en otra.
Sin embargo, esta representación de árbol crecerá infinitamente si el número de tokens en cada lugar de la red aumenta de manera ilimitada. Para mantener un árbol finito, se incluye un símbolo especial ω, el cual representará a aquellos lugares cuyo número de tokens crezca de manera infinita. Además, ω tiene la propiedad de que para cada n, ω > n, ω ± n = ω y ω >= ω.
Ecuación de Estado. El comportamiento dinámico de muchos sistemas estudiados en ingeniería puede ser descrito por ecuaciones diferenciales o por ecuaciones algebraicas. Sería agradable si pudiésemos describir y analizar completamente el comportamiento dinámico de las RdP con algunas ecuaciones. Con este propósito se desarrollaron ecuaciones de estado que rigen el comportamiento dinámico de los sistemas concurrentes que son modelados con RdP. Sin embargo, la factibilidad de estas ecuaciones es limitada, debido a la naturaleza no determinista inherente a las RdP y a la restricción de que en las soluciones deben encontrarse sólo números no negativos. [7]
Reglas de simplificación de RdP. Para facilitar el análisis de sistemas grandes, es común reducir el modelo del sistema a uno más sencillo, mientras se mantengan las propiedades del sistema que se está analizando. Por el contrario, las técnicas para transformar un modelo abstracto en un modelo más refinado de manera jerárquica se pueden utilizar para síntesis. Existen muchas técnicas de transformación en RdP, las cuales se describen en [5].
Simulación de una RdP. Para modelos de RdP complejos, la simulación de eventos discretos es otra forma de verificar las propiedades del sistema. La idea es simple, se disparan las transiciones que se encuentren habilitadas, actualizando el número de tokens en los lugares de entrada y salida de las transiciones disparadas. Se sigue este esquema hasta que ya no exista alguna transición habilitada o se establezca un criterio de parada. De esta manera podemos checar el comportamiento que sigue el sistema al establecer ciertas condiciones de entrada en la marca de inicio.
Existen sistemas de eventos discretos cuya modelación con las RdP descritas anteriormente se vuelve complicado, debido a características presentes en estos sistemas que no son fáciles de incorporar. Tal es el caso de sistemas donde está presente la aleatoriedad en la ocurrencia de eventos, o aquellos donde se necesita contar con atributos de estos eventos para hacer una representación más cercana a la realidad. Por tal motivo, al modelo original de RdP se le han incorporado características que permitan la modelación y simulación de estos sistemas. Entre los modelos extendidos de RdP que se han propuesto están las RdP Temporizadas, RdP estocásticas, RdP Coloreadas, RdP Difusas, RdP Coloreada Condicional, etc. [6][8] [9] [10].
Red de Petri Temporizada. Se introdujeron para modelar sistemas donde se necesita que el disparo de una transición considere un retardo en el tiempo para denotar el uso de servidores y su tiempo de servicio o procesamiento.
Red de Petri Estocástica. Se aplican cuando el retardo aplicado a una transición toma en cuenta una variable aleatoria, determinada por un función de densidad de distribución.
Red de Petri Coloreada. Es un tipo de RdP extendida donde los tokens corresponden a un color determinado. El color del token corresponde a un tipo de dato que tiene asignado el token, pudiendo ser estructuras de datos completas las que se encuentran en cada token. La información alojada en cada token fluye a través del disparo de las transiciones, de acuerdo a la dinámica que se presenta en un sistema real.
Red de Petri Difusa. Se desarrolló para poder manejar conceptos de lógica difusa, donde una transición habilitada puede disparar si el valor del token cumple con el umbral definido en la transición. Este tipo de RdP son utilizadas en la definición de reglas de producción aplicadas en sistemas expertos.
Red de Petri Coloreada Condicional. Esta extensión de RdP fue desarrollada con la finalidad de definir reglas de tipo ECA (Evento-Condición-Acción), utilizadas en los Sistemas de Bases de Datos Activas. Al igual que una RdP Coloreada, los tokens almacenan información, correspondientes a los registros de las bases de datos, sin embargo, en esta RdP se aplica una evaluación en la transición donde se almacena la parte condicional de la regla ECA.
A continuación se desarrollan dos ejemplos de la aplicación de las RdP en sistemas de eventos discretos, uno aplicado en un sistema de manufactura flexible, y el otro a un sistema de protocolo de comunicación.
Modelo de brazo de robot. Este ejemplo considera un sistema de manufactura flexible (figura 2) donde se tiene una banda transportadora por donde arriban piezas para ser procesadas, estas piezas son tomadas por un brazo de robot que las deposita en una máquina para su procesamiento. Al finalizar el proceso, el brazo de robot vuelve a tomar la pieza para depositarla en una banda de salida. [8].
Figura 2. Sistema de manufactura flexible.
La RdP correspondiente al sistema de la figura 2 se presenta en la figura 3, donde los estados que se presentan en el sistema se denotan como lugares de la RdP.
Figura 3. RdP correspondiente a los estados del sistema de manufactura flexible.
El estado inicial del sistema modelado por la RdP de la figura 3, indica que existe una pieza en la banda de entrada (p1), que el brazo de robot está listo para tomar alguna pieza (p2) y que la máquina de proceso también está disponible (p4). El marcado de este estado sería M0 = (1 1 0 1 0 0 0), que corresponden a los tokens de los lugares M0 = (p1 p2 … p7), respectivamente. Bajo estas condiciones, la transición t1 se encuentra habilitada, es decir, para que una pieza sea tomada por el brazo de robot es necesario que la pieza se encuentre en la banda de entrada y el brazo de robot se encuentre disponible.. En la figura 4(a) se muestra el estado de la RdP M1 = (0 0 1 1 0 0 0) después del disparo de t1, que indica que la pieza está tomada por el brazo del robot y la máquina de procesamiento aún se encuentra disponible. La figura 4(b) muestra el estado M2 = (0 1 0 0 1 0 0), obtenido después del disparo de t2, donde el brazo de robot está ahora disponible y la máquina de procesamiento se encuentra en operación.
Figura 4. Disparo de transiciones en la dinámica del sistema real. (a) después del disparo de t1. (b) después del disparo de t2. (c) después del disparo de t3. (d) después del disparo de t4.
La figura 4(c) indica el estado alcanzado después del disparo de t3, M3 = (0 0 0 1 0 1 0), donde el brazo de robot ha tomado la pieza de la máquina de procesamiento y ésta se encuentra disponible. Finalmente, la figura 4(d) muestra el estado del sistema con el marcado M4 = (0 1 0 1 0 0 1), después del disparo de la transición t4, donde la pieza ha sido colocada en la banda de salida, y tanto el brazo de robot como la máquina de procesamiento se encuentran disponibles. A partir del marcado M4 se habilita la transición t5, cuyo disparo generaría el marcado M0, el cual corresponde al estado inicial del sistema.
Modelo de protocolo de comunicación aplicando RdP Coloreada. Ahora consideramos un ejemplo sencillo de un protocolo de comunicaciones, donde se envían paquetes de datos entre un emisor y un receptor. Para modelar este sistema se utiliza una RdP Coloreada, debido a que se necesita enviar información a través de la RdP (figura 5). [9]
Figura 5. RdP Coloreada para el modelo de protocolo de comunicación.
Los lugares “Paquetes para enviar”, A, “B” y “Paquetes recibidos” son de tipo NUMxDATO, es decir, almacenan tokens que tienen una estructura formada por un número y un texto. Mientras que los lugares “C”, “D” y “Siguiente envío” son de tipo NUM, ya que pueden almacenar tokens que contengan un valor numérico. El estado inicial de esta RdP Coloreada indica que el lugar “Paquetes para enviar contiene 6 tokens diferentes, y el lugar “Siguiente envío” contiene un token con un valor de 1. Con este estado inicial, la transición “Enviar paquete” se encuentra habilitada, y al dispararse tomaría el token (1,”RED “) del lugar “Paquetes para enviar” y el token 1 del lugar “Siguiente envío”, ya que son los que coincidirían en el valor n denotado en los arcos de entrada a la transición “Enviar paquete”. El token (1,”RED”) pasaría al lugar “A”. Posteriormente se dispara la transición “Transmitir paquete” y se sigue enviando el mismo token al lugar “B”. Después se dispara la transición “Recibir paquete”, enviando el token (1,”RED “) al lugar de salida “Paquetes recibidos” y a la vez envía un token al lugar “C”, donde el token enviado a “C” sería el valor de n+1, dando como resultado un token con valor de 2. Este token genera el disparo de la transición “Transmitir acuse de recibo”, la cual deposita el token con valor 2 en el lugar “D”. A su vez, el token en el lugar “D” provoca el disparo de la transición “Recibir acuse de recibo” y se envía el token con valor 2 al lugar “Siguiente envío”. En este estado se continúa con el disparo de la transición “Enviar paquete”, pero ahora se tomaría el token (2,”DE P”) del lugar “Paquetes para enviar”, y se sigue la misma dinámica descrita para el token (1,”RED “).
Es importante desarrollar modelos de los sistemas de eventos discretos para estudiarlos y comprender su comportamiento. Existen herramientas computacionales que permiten analizar este tipo de sistemas, las cuales están basadas en análisis estadísticos y ofrecen soluciones con ciertos grados de incertidumbre.
Por otro lado, las RdP pueden ser aplicadas para la modelación de sistemas de eventos discretos, las cuales ofrecen una forma de representación gráfica y matemática de los sistemas modelados. La formalidad matemática de la RdP proporcionan herramientas de análisis para analizar los posibles estados a los que el sistema modelado pudiera alcanzar.
Además, existen extensiones de RdP para modelar sistemas que no puedan ser representados fácilmente con las RdP tradicionales. Por lo tanto, si existe algún sistema de evento discreto que no pudiera modelarse con las RdP propuestas por diferentes investigadores, es posible adecuar el modelo original, adicionarle las características necesarias, y proponer una nueva extensión de RdP.
[1]Harrel, C.R., Ghosh, B.K., Bowden, R.O. 2009. Simulation Using Promodel. McGraw-Hill, 2nd Edition.
[2]Altiok, T., Melamed, B. 2007. Simulation, Modeling and Analysis with Arena. Elsevier, 1st. Edition.
[3]Beaverstock, M., Greenwood, A., Lavery, E., Nordgren, W. Applied Simulation, Modeling and Analysis using FlexSim. Flexsim Products, 3rd Edition.
[4]Petri, C.A. 1962. Kommunikation mit Automaten. Schriften des IIM Nr. 3. Institute für Instrumentelle Mathematik, Bonn. English translation: Communication with Automata. Tech Rep. RADC-TR-65-377, vol 1, 1966. Griffiss Air Force Base, New York.
[5]Murata, T. 1989. Petri Nets: Properties, Analysis and Applications. Proceedings of the IEEE, 77(4): 541-580.
[6]Li, X., Lara-Rosano, F. 2000. Adaptive Fuzzy Petri Nets for Dynamic Knowledge Representation and Inference. Expert System with Applications 19: 235-241.
[7]Wang J. 1998. Timed Petri Nets. Theory and Applications. Kluwer Academic Publishers.
[8]Zhou, M., Venkatesh, K., 1999. Modeling, Simulation, and Control of Flexible Manufacturing Systems. Series in Intelligent Control and Intelligent Automation 6, World Scientific Publishing.
[9]Jensen, K., Kristensen, L. 1998. Coloured Petri Nets. Springer.
[10]Li, X., Medina-Marin, J., Chapa-Vergara, S.V. 2007. Applying Petri nets in Active Databases. IEEE Transactions on Systems, Man and Cybernetics – Part C: Applications and Reviews 37(4): 482 – 493.
[a1]Recibió los grados de Maestría y Doctorado en Ciencias en Ingeniería Eléctrica opción Computación por el Centro de Investigación y de Estudios Avanzados (CINVESTAV) del Instituto Politécnico Nacional, en 2002 y 2005, respectivamente. Actualmente se desempeña como Profesor Investigador del Centro de Investigación Avanzada en Ingeniería Industrial en el Área Académica de Ingeniería de la UAEH. Sus líneas de investigación incluyen la teoría de redes de Petri y sus aplicaciones, bases de datos activas, y simulación de sistemas de eventos discretos.
[a2]Recibió los grados de Maestría y Doctorado en Ciencias en Ingeniería Eléctrica (opción Computación) por parte del Centro de Investigación y de Estudios Avanzados del Instituto Politécnico Nacional en México, en 1999 y 2002, respectivamente. Actualmente es Profesor del Centro de Investigación Avanzada en Ingeniería Industrial en la Universidad Autónoma del Estado de Hidalgo, en Pachuca, Hidalgo, México. Sus intereses actuales de investigación incluyen teoría de autómatas celulares y sus aplicaciones, computación evolutiva y simulación.
[a3]Recibió en grado de Maestro en Ciencias en el Departamento de Ingeniería Eléctrica del Instituto Tecnológico de La Laguna en México, en el año de 2001; y el grado de Doctor en Ciencias en ingeniería Industrial por parte de la Universidad Autónoma del Estado de Hidalgo, en Pachuca, Hidalgo, México. Sus intereses de investigación actuales incluyen la identificación de sistemas, el diseño de controles, algoritmos genéticos, lógica difusa, y redes neuronales y sus aplicaciones.