Stochastic Dynamic Programming Model for the Quality Deterioration of an Unreliable Manufacturer
Modelo de programación dinámica estocástico para el deterioro de la calidad de un sistema de manufactura no fiable
Héctor Rivera-Gómez [a][*], Oscar Montaño-Arango[b]
, José Ramón Corona-Armenta[c]
, Eva Selene Hernández-Gress[d]
Área Académica de Ingeniería, Instituto de Ciencias Básicas e Ingeniería, Universidad Autónoma del Estado de Hidalgo, Carr. Pachuca-Tulancingo Km 4.5, Ciudad del Conocimiento, Col. Carboneras, C. P. 42184, Pachuca de Soto, Hgo., México.
Resumen
Este artículo propone un nuevo modelo integrador que analiza puntos sobre el fenómeno de degradación en el control óptimo de un sistema de manufactura no fiable. El sistema bajo estudio estuvo compuesto de una máquina, sujeta a fallas y reparaciones aleatorias, que producía un tipo de pieza con demanda constante. Además, la máquina experimentó una degradación progresiva la cual se reflejó principalmente en el aumento de la tasa de defectivos. El mantenimiento mayor estuvo disponible como una contramedida para mitigar el efecto de la degradación de la calidad. Dada la importancia que tienen el inventario, los pedidos pendientes y el costo de mantenimiento; el objetivo principal del artículo fue desarrollar un controlador que considerara la degradación de la calidad y definiera conjuntamente estrategias de producción y mantenimiento a fin de minimizar el costo total incurrido. La estructura de dicho controlador se definió a través de técnicas numéricas. Los resultados obtenidos mostraron la fuerte interacción de la degradación en el controlador.
Palabras clave: Control de la producción, simulación, sistemas de manufactura, defectos, programación dinámica.
Abstract
This paper proposes a new integrated model, which analyses deteriorations issues in the optimal control of an unreliable production system. The system under concern was composed of a machine subject to random failures, and repairs, which produced a part type with constant demand. Furthermore, the machine was subject to progressive deterioration reflected mainly in an increasing rate of defectives. Major maintenance such as overhaul was available as a countermeasure to mitigate the effect of the quality deterioration. Given the importance of inventory, backlog and maintenance cost, the main objective of the paper was to develop a control policy, which considered quality deterioration and states the joint production and overhaul strategies to minimize the total incurred cost. The structure of the joint control policy was defined through numerical techniques. The obtained results showed the strong influence of deterioration issues in the optimal control policy.
Keywords: Production control, simulation, manufacturing systems, defectives, dynamic programming
Introduction
Production planning has been studied by several authors, with the common objective of improving productivity. However, a major limitation encountered in most of the literature in this domain lies in the assumption that all parts produced are conforming items; an assumption, which is obviously not realistic in industrial contexts. Fortunately, the inter-relation between productivity and quality has been received growing attention of researchers. We started by examining the need to integrate quality aspects in production policies, since all companies must satisfy high levels of productivity and high standards of quality. Additionally, if we take into account that manufacturing systems progressively degrade over time means that, this factor may have an impact on its operating conditions. Therefore, through this research, we contributed to a better understanding of the inter-relation between production planning and quality, in the case where the manufacturing system is subject to deterioration, which has a negative influence on the quality of parts produced.
A recent area of research has emerged addressing quality issues on the production policy. Radhoui et al. (2009), for instance, used the rate of defectives as a decision variable to determine when to perform preventive maintenance and define the buffer size. The simultaneous determination of maintenance activities and production planning was covered by Njike et al. (2009), applying several operational states that monitor the condition of the systems. They used the quantity of defective products as feedback to optimally control the system. Further, Mhada et al. (2011) analyzed the production control problem for an unreliable manufacturing system producing a random fraction of defective items, and succeeded in stating analytical expressions for the production threshold and the optimal cost. Additionally Dhouib et al. (2012) incorporates to the production planning problem, an age-dependent preventive maintenance policy that reduces the shift rate to the out of control state, where their productive systems produces non-conforming items. Despite the pertinence of these works, we conjecture that the joint production and quality control problem can be studied from a different perspective. For instance, this includes bearing in mind that in real industrial contexts, the production system is subject to deteriorations (because of an infinite set of factors), meaning therefore that the effect of the deterioration may certainly have an impact on the quality of the parts produced. This effect will allow us to extend the concept of deterioration, and relate this factor to the quality yield of the production system. We find some support for our conjecture in the area of deteriorating systems.
Many papers have been published in the area of deteriorating systems, with the typical method used to model deterioration based on the concept of imperfect maintenance. A good discussion on the subject of imperfect maintenance can be found in Pham and Wang (1996). In addition, Wang and Pham (1999) presented an interesting method, and proposed that after an imperfect repair, the operating time of the system decreased as the number of repairs increased. The idea to treat certain deterioration in the operating conditions was extended by Lam (2007), who proposed that the operating times after a repair decreased, while the consecutive repair times after failure increased. We found another approach for modeling deteriorating systems in the work of Dehayem et al. (2011), who described a model in which the operating time of the production system followed a decreasing function given by the age of the machine, while the repair time consisted of an increasing function with the number of failures. As it can be seen from the previous models, it was assumed that deterioration had an effect on the availability of the production system, and that it was used as indicator of the level of deterioration either the age of the machine or the number of failures. Nevertheless, in these models the degrading process was not linked with the parts quality. This observation in turn raised the question of whether it is possible to relate the deterioration phenomenon with the quality yield of the production system. Typically, an efficient alternative for determining the optimal control policies of stochastic manufacturing systems has been the use of simulation optimization approaches.
Therefore, given this context, we intended to develop a new model for the simultaneous production and quality control policy of a mono-product manufacturing system, composed of a single unreliable machine that was subject to progressive quality deterioration and uncertainties. The resultant control policy called Machine Deterioration Dependent Hedging Point Policy (MDDHPP), adjusted the control parameters according to the level of deterioration of the machine. The contribution of this article is further illustrated by the robust behavior of the MDDHPP, and providing a better knowledge of the production system behavior.
The remainder of the paper was structured as follows. After an overview of the literature in section 1, the control problem statement is detailed in section 2. Numerical methods are applied to characterize the structure of the obtained control policy in section 3. Finally, concluding remarks that illustrate new insights into this topic are given in section 4.
Control Problem Formulacion
The system is subject to random events (failures, repairs, and overhauls) as well as to quality deterioration. The machine has three modes, described by the stochastic process 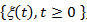 , with values in
, with values in 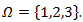 , The machine is available when operational
, The machine is available when operational 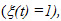 , and unavailable when under repair
, and unavailable when under repair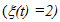 or under overhaul
or under overhaul 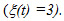 . The overhaul refers to a perfect maintenance whose benefit is to counter quality deterioration and restore the machine to as-good-as-new conditions.
. The overhaul refers to a perfect maintenance whose benefit is to counter quality deterioration and restore the machine to as-good-as-new conditions.
According to standard notation, let d be the demand to be satisfied and 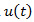 the production rate at time t. At any time instant, the production rate
the production rate at time t. At any time instant, the production rate 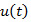 of the machine has to satisfy the capacity constraint:
of the machine has to satisfy the capacity constraint: 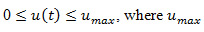 is the maximum production rate.
is the maximum production rate.
We proposed that the dynamics of the inventory/backlog of products x(t) evolves according to the following differential equation:
Where 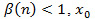 is the initial stock level, n is the current number of failures at time
is the initial stock level, n is the current number of failures at time 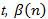 function of the rate of defectives, and the quantity
function of the rate of defectives, and the quantity 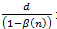 represents the adjusted demand that includes defective products
represents the adjusted demand that includes defective products
We extend the concept of worse repairs to model quality deterioration, and based on the relationships between failures-deterioration and deterioration-quality, we propose the increasing function (2), which defines the rate of defectives as a function of the number of failures, as follows:
Where 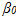 is the value of the rate of defectives at initial conditions (normally with a very low value), N is the number of failures where the system is still operational, and
is the value of the rate of defectives at initial conditions (normally with a very low value), N is the number of failures where the system is still operational, and 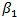 and rare given parameters.
The manufacturing system will only meet the conditions needed to fulfill the demand rate d over an infinite horizon, and reach steady-state, only if the system is feasible. In other words, the production system must satisfy the following feasibility condition:
and rare given parameters.
The manufacturing system will only meet the conditions needed to fulfill the demand rate d over an infinite horizon, and reach steady-state, only if the system is feasible. In other words, the production system must satisfy the following feasibility condition:
Where, 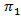 is the limiting probability for the operational state. Let
is the limiting probability for the operational state. Let 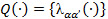 refer to the related transition matrix. Therefore
refer to the related transition matrix. Therefore 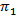 can be computed as follows:
can be computed as follows:
For our case of study, the solution of 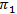 for the system of equations (4) yields to the following expression:
for the system of equations (4) yields to the following expression:
Where 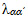 are the transition rates from mode a to mode
are the transition rates from mode a to mode 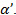 . In a practical sense, the value of the parameters needed by equation (2) can be determined from the analysis of maintenance service data.
. In a practical sense, the value of the parameters needed by equation (2) can be determined from the analysis of maintenance service data.
The machine’s mode changes from operation mode to overhaul mode with a transition rate denoted by 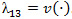 The rate
The rate 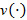 is assumed to be a control variable. The inverse of
is assumed to be a control variable. The inverse of 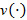 represents the expected delay time between the decision to perform the overhaul and the effective switch from operation mode to overhaul mode. Moreover, we assume that the following constraint holds for the overhaul rate:
represents the expected delay time between the decision to perform the overhaul and the effective switch from operation mode to overhaul mode. Moreover, we assume that the following constraint holds for the overhaul rate:
Where 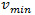 and
and 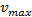 denote the minimum and maximum overhaul rate, respectively. The instantaneous cost function of the model at mode a
denote the minimum and maximum overhaul rate, respectively. The instantaneous cost function of the model at mode a 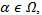 , is defined by the following equation:
, is defined by the following equation:
With
Where 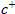 + is the inventory cost,
+ is the inventory cost, 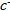 is the backlog cost, cr is the repair cost
is the backlog cost, cr is the repair cost 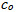 is the overhaul cost. The control variables of the model are the production rate
is the overhaul cost. The control variables of the model are the production rate 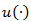 and the overhaul rate
and the overhaul rate 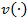 the set of admissible decisions
the set of admissible decisions 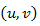 depends on the stochastic process and, is given by:
depends on the stochastic process and, is given by:
Our objective is to control the production rate 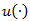 and the overhaul rate
and the overhaul rate 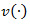 in order to minimize the integral of the expected discounted cost given by:
in order to minimize the integral of the expected discounted cost given by:
Where p is the discounted rate and (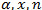 ) are the initial state conditions. Optimal policies are obtained by searching in the value function:
) are the initial state conditions. Optimal policies are obtained by searching in the value function:
The value function 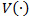 satisfies the so-called Hamilton-Jacobi-Bellman (HJB) equations. Such equations describe the optimally conditions of the problem. In this case, the derivation of the optimality conditions leads to the following HJB equations:
satisfies the so-called Hamilton-Jacobi-Bellman (HJB) equations. Such equations describe the optimally conditions of the problem. In this case, the derivation of the optimality conditions leads to the following HJB equations:
Where 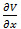 is the derivative of the value function. Because of the randomness of a, the control policy is a feedback control rule based on the inventory level x, the mode of the machine a, and the number of failures n. Furthermore, as the overhaul activity restores the rate of defectives
is the derivative of the value function. Because of the randomness of a, the control policy is a feedback control rule based on the inventory level x, the mode of the machine a, and the number of failures n. Furthermore, as the overhaul activity restores the rate of defectives 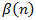 to initial conditions, at a jump time τ for the process
to initial conditions, at a jump time τ for the process 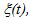 , we define a reset function
, we define a reset function 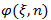 by the following relationship:
by the following relationship:
We conclude this section by stating that, in general, solving the HJB equations is usually impractical. Fortunately, Boukas and Haurie (1990) implemented the Kushner’ method to solve such a problem in the context of production planning. In the next section, we detail the procedure for determining control policies.
Control Policy
To determine the optimal policy, a solution could be approximated with the HJB equations by the application of numerical methods based on the Kushner technique. The main idea of this approach is to use an approximation scheme for the gradient of the value function V(a,x,n). More details about the numerical method can be consulted in Kushner and Dupuis (1992) and in Hajji et al. (2009), and references therein.
Table 1 presents the value for the set of parameters used in the numerical example. From the literature of optimal control and maintenance it is customary to assume that the cost of negative inventory is much higher than the cost of positive inventory 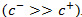 . Furthermore, it is normal that the overhaul cost is higher than the repair cost
. Furthermore, it is normal that the overhaul cost is higher than the repair cost 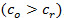 . Without loss of generality data of Table 1 satisfies the feasibility condition until the 20th failure
. Without loss of generality data of Table 1 satisfies the feasibility condition until the 20th failure
Table 1: Parameters of the numerical example
| Parameter |
umax |
d |
H |
ρ |
c+ |
c- |
| Value |
5 |
3 |
0.5 |
0.9 |
5 |
250 |
| Parameter |
cr |
co |
N |
r |
β0 |
β1 |
| Value |
5 |
10 |
20 |
1 |
0 |
0.35 |
| Parameter |
λ12 |
λ21 |
λ31 |
vmin |
vmax |
|
| Value |
0.1 |
2 |
0.6 |
0.0001 |
20 |
|
The optimal production threshold level is denoted by 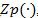 , and defines the limits of the production region. The production control policy obtained is an extension of the Hedging Point Policy.
, and defines the limits of the production region. The production control policy obtained is an extension of the Hedging Point Policy.
In this case due to the effect of the deterioration of the parts quality; the production policy leads to the following Machine Deterioration Dependent Hedging Point Policy (MDDHPP):
Where 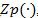 is the funtion that gives the optimal production threshold for each failure n. We note that the production threshold
is the funtion that gives the optimal production threshold for each failure n. We note that the production threshold 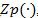 , increases progressively. The overhaul policy identifies two zones in the computational domain delimited by the boundary
, increases progressively. The overhaul policy identifies two zones in the computational domain delimited by the boundary 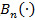 , as follows:
, as follows:
- Zone A: in this zone the quality deterioration, denoted by the number of failures, has a high level, which justifies the cost of performing an overhaul, and thus the overhaul rate is set to its maximum value,
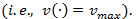
- Zone B: here the quality deterioration is low, meaning that an overhaul is not recommended, and the related decision variable is set to its minimum value,
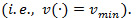
According to the obtained results of the numerical method, it is clear that the overhaul policy has a bang-bang structure. Moreover, the overhaul activity is triggered according to the following policy, which indicates that the overhaul activity should be performed at rate 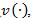 , with:
, with:
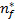 is the number of failures limit required to conduct the overhaul. For a given number of failures n, the parameter
is the number of failures limit required to conduct the overhaul. For a given number of failures n, the parameter 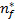 is the point where the production threshold
is the point where the production threshold 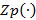 intersects the overhaul zone 𝐴. Summing up, we can illustrate the joint production and overhaul policies by equations (13)-(14), which are characterized by the control parameters
intersects the overhaul zone 𝐴. Summing up, we can illustrate the joint production and overhaul policies by equations (13)-(14), which are characterized by the control parameters 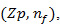 where
where 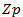 corresponds to the value of
corresponds to the value of 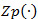 for each n value.
for each n value.
Conclusions
In this paper, issues pertaining to the inter-relation between production control and quality aspects are investigated in a manufacturing system consisting of an unreliable single machine, single part type manufacturing system. The machine is subject to deteriorations that have a negative effect on the quality of the parts produced, a fact that is especially reflected in the rate of defectives. The quality issues are related with the overhaul strategy, since it counters the effect of the deterioration. We investigate the structure of the joint production and overhaul control policy through the application of numerical methods designed for stochastic optimal control models. The resulting policy consists of a Machine Deterioration Dependent Hedging Point Policy which controls the production rate, and comprises several increasing thresholds and an overhaul strategy that performs a perfect repair when the number of failures is high. This leads to the identification of the two associated control parameters of the joint control policy as dependent on the deterioration of the production system.
References
Boukas, E.K., Hauire, A. (1990) Manufacturing flow control and preventive maintenance: a stochastic control approach. IEEE Transactions on Automatic Control, 33, 1024-1031.
Dehayem Nodem, F.I., Kenné, J.P., Gharbi, A. (2011) Simultaneous control of production, repair/replacement and preventive maintenance of deteriorating manufacturing systems. International Journal of Production Economics, 134, 271-282.
Dhouib, K., Gharbi, A., Ben Aziza, M.N. (2012) Joint optimal production control/preventive maintenance policy for imperfect process manufacturing cell. International Journal of Production Economics, 137, 126-136.
Hajji, A., Gharbi, A., Kenné, J.P. (2009) Joint replenishment and manufacturing activities control in two stages unreliable supply chain. International Journal of Production Research, 47 (12), 3231-3251.
Kushner, H.J., Dupuis, P.G. (1992) Numerical Methods for Stochastic Control Problems in Continuous Time, Springer, New York, NY.
Lam, Y., Zhu, L.X., Chan, J.S.K., Liu, Q. (2004) Analysis of data from a series of events by a geometric process model, Acta Mathematicae Applicatae, 20, 263-282.
Lam, Y. (2007) A geometric process maintenance model with preventive repair. European Journal of Operation Research, 182, 806-819.
Mhada, F., Hajji, A., Malhame, R., Gharbi, A., Pellerin, R. (2011) Production control of unreliable manufacturing systems producing defective items, Journal of Quality in Maintenance Engineering, 17( 3), 238-253.
Njike, A.N., Pellerin, R., Kenné, J.P. (2009) Simultaneous control of maintenance and production rates of a manufacturing system with defective products. Journal of Intelligent Manufacturing, 10845, article 354.
Pham, H., Wang H. (1996) Imperfect maintenance, European Journal of Operation Research, 94, 425-438.
Radhoui, M., Rezg, N., Chelbi, A. (2009) Integrated model of preventive maintenance, quality control and buffer sizing for unreliable and imperfect production systems. International Journal of Production Research, 47( 2), 389-402.
Wang, H. (2002) A survey of maintenance policies of deteriorating systems. European Journal of Operation Research, No. 139, 468-489.
Wang, H., Pham, H. (1999) Some maintenance models and availability with imperfect maintenance in production systems, Annual of Operation Research, 91, 305-318.
[a] Dr. Héctor Rivera-Gómez: Recibió el grado de doctor por parte de la Ecolé du Technologie Superieure de la Universidad de Quebec, en Montreal Canadá. Actualmente es profesor investigador del ICBI, miembro del Sistema Nacional de Investigadores y del cuerpo académico de Ingeniería de Sistemas Organizacionales, cuenta con el perfil deseable Promep. Sus intereses de investigación tratan sobre el análisis y modelación de sistemas productivos.
[b] Dr. Oscar Montaño-Arango: Cuenta con el grado de doctor en ingeniería con especialidad en sistemas de planeación por parte de la UNAM. Es Profesor-investigador de la UAEH, y miembro del Sistema Nacional de Investigadores Nivel 1. Es el líder del cuerpo académico de Ingeniería de Sistemas Organizacionales.
[c] Dr. José Ramón Corona-Armenta: Cuenta con el grado de doctor en ingeniería, con énfasis en ingeniería de sistemas industriales del Instituto nacional Politécnico de Lorena en Francia. Es profesor-investigador del ICBI, miembro del Sistema Nacional de investigadores. Sus áreas de interés son la innovación tecnológica, desarrollo sustentable y prospectiva.
[d]Dr. Eva Selene Hernández-Gress: Obtuvo el grado de Doctor en Ingeniería Industrial por parte de la UAEH y cuenta con una Maestría en Ciencias con Especialidad en Ingeniería Industrial en el Tecnológico de Monterrey, Campus Estado de México. Es miembro del Sistema Nacional de Investigadores y actualmente profesor-investigador del Área Académica de Ingeniería.
[*] Corresponding author: hriver06@hotmail.com
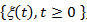 , with values in
, with values in 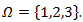 , The machine is available when operational
, The machine is available when operational 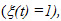 , and unavailable when under repair
, and unavailable when under repair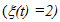 or under overhaul
or under overhaul 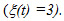 . The overhaul refers to a perfect maintenance whose benefit is to counter quality deterioration and restore the machine to as-good-as-new conditions.
. The overhaul refers to a perfect maintenance whose benefit is to counter quality deterioration and restore the machine to as-good-as-new conditions. 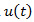 the production rate at time t. At any time instant, the production rate
the production rate at time t. At any time instant, the production rate 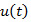 of the machine has to satisfy the capacity constraint:
of the machine has to satisfy the capacity constraint: 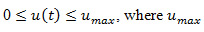 is the maximum production rate.
is the maximum production rate.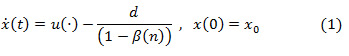
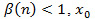 is the initial stock level, n is the current number of failures at time
is the initial stock level, n is the current number of failures at time 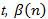 function of the rate of defectives, and the quantity
function of the rate of defectives, and the quantity 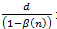 represents the adjusted demand that includes defective products
represents the adjusted demand that includes defective products 
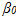 is the value of the rate of defectives at initial conditions (normally with a very low value), N is the number of failures where the system is still operational, and
is the value of the rate of defectives at initial conditions (normally with a very low value), N is the number of failures where the system is still operational, and 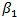 and rare given parameters.
The manufacturing system will only meet the conditions needed to fulfill the demand rate d over an infinite horizon, and reach steady-state, only if the system is feasible. In other words, the production system must satisfy the following feasibility condition:
and rare given parameters.
The manufacturing system will only meet the conditions needed to fulfill the demand rate d over an infinite horizon, and reach steady-state, only if the system is feasible. In other words, the production system must satisfy the following feasibility condition: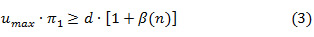
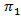 is the limiting probability for the operational state. Let
is the limiting probability for the operational state. Let 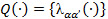 refer to the related transition matrix. Therefore
refer to the related transition matrix. Therefore 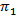 can be computed as follows:
can be computed as follows: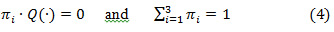
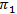 for the system of equations (4) yields to the following expression:
for the system of equations (4) yields to the following expression: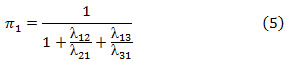
 are the transition rates from mode a to mode
are the transition rates from mode a to mode 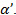 . In a practical sense, the value of the parameters needed by equation (2) can be determined from the analysis of maintenance service data.
. In a practical sense, the value of the parameters needed by equation (2) can be determined from the analysis of maintenance service data.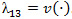 The rate
The rate 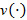 is assumed to be a control variable. The inverse of
is assumed to be a control variable. The inverse of 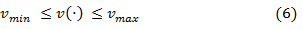
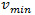 and
and 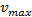 denote the minimum and maximum overhaul rate, respectively. The instantaneous cost function of the model at mode a
denote the minimum and maximum overhaul rate, respectively. The instantaneous cost function of the model at mode a 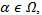 , is defined by the following equation:
, is defined by the following equation: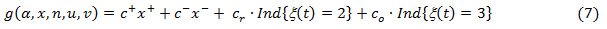
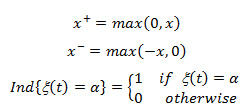
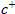 + is the inventory cost,
+ is the inventory cost, 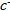 is the backlog cost, cr is the repair cost
is the backlog cost, cr is the repair cost 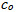 is the overhaul cost. The control variables of the model are the production rate
is the overhaul cost. The control variables of the model are the production rate 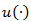 and the overhaul rate
and the overhaul rate 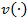 the set of admissible decisions
the set of admissible decisions 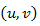 depends on the stochastic process and, is given by:
depends on the stochastic process and, is given by: 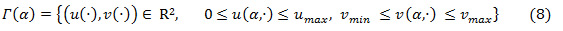
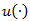 and the overhaul rate
and the overhaul rate 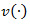 in order to minimize the integral of the expected discounted cost given by:
in order to minimize the integral of the expected discounted cost given by: 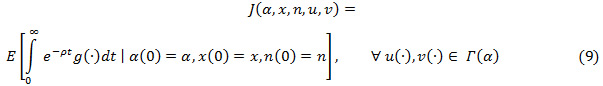
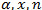 ) are the initial state conditions. Optimal policies are obtained by searching in the value function:
) are the initial state conditions. Optimal policies are obtained by searching in the value function: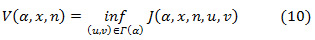
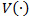 satisfies the so-called Hamilton-Jacobi-Bellman (HJB) equations. Such equations describe the optimally conditions of the problem. In this case, the derivation of the optimality conditions leads to the following HJB equations:
satisfies the so-called Hamilton-Jacobi-Bellman (HJB) equations. Such equations describe the optimally conditions of the problem. In this case, the derivation of the optimality conditions leads to the following HJB equations: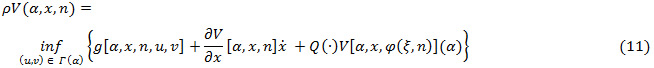
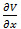 is the derivative of the value function. Because of the randomness of a, the control policy is a feedback control rule based on the inventory level x, the mode of the machine a, and the number of failures n. Furthermore, as the overhaul activity restores the rate of defectives
is the derivative of the value function. Because of the randomness of a, the control policy is a feedback control rule based on the inventory level x, the mode of the machine a, and the number of failures n. Furthermore, as the overhaul activity restores the rate of defectives 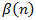 to initial conditions, at a jump time τ for the process
to initial conditions, at a jump time τ for the process 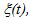 , we define a reset function
, we define a reset function 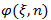 by the following relationship:
by the following relationship: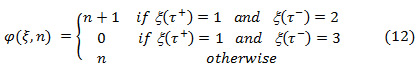
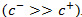 . Furthermore, it is normal that the overhaul cost is higher than the repair cost
. Furthermore, it is normal that the overhaul cost is higher than the repair cost 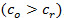 . Without loss of generality data of Table 1 satisfies the feasibility condition until the 20th failure
. Without loss of generality data of Table 1 satisfies the feasibility condition until the 20th failure
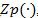 , and defines the limits of the production region. The production control policy obtained is an extension of the Hedging Point Policy.
, and defines the limits of the production region. The production control policy obtained is an extension of the Hedging Point Policy.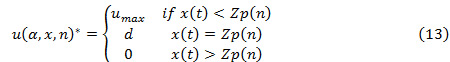
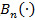 , as follows:
, as follows: 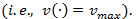
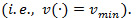
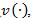 , with:
, with: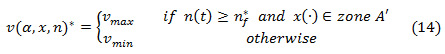
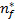 is the number of failures limit required to conduct the overhaul. For a given number of failures n, the parameter
is the number of failures limit required to conduct the overhaul. For a given number of failures n, the parameter 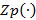 intersects the overhaul zone 𝐴. Summing up, we can illustrate the joint production and overhaul policies by equations (13)-(14), which are characterized by the control parameters
intersects the overhaul zone 𝐴. Summing up, we can illustrate the joint production and overhaul policies by equations (13)-(14), which are characterized by the control parameters 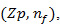 where
where 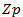 corresponds to the value of
corresponds to the value of 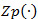 for each n value.
for each n value.