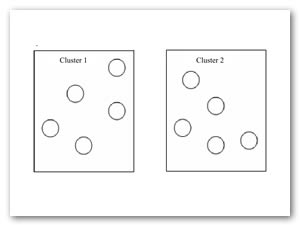
Figura 1. Agrupación de Cromosomas en K clústeres.
El presente trabajo de investigación busca resolver el bien conocido Problema del Agente Viajero, utilizando para ello los algoritmos genéticos, dividiendo al problema en cuestión a través de agrupaciones denominadas clústeres, con la intensión de reducir el número de nodos al momento de aplicar los algoritmos genéticos. Es por ello que se propone un método para estructurar los clústeres, definiendo inicialmente K puntos llamados centroides en cada uno de los K clústeres, para posteriormente recalcular a los centroides en cuestión, de tal manera que la distancia entre cada uno de estos en su respectivo clúster y cada uno de los nodos, sea la mínima, hasta el punto en que los centroides no se muevan más; para posteriormente aplicar algoritmos genéticos a cada uno de ellos en busca de minimizar las distancias, para finalmente unir a cada uno de los clústeres con un método también propuesto y con ello llegar a una buena solución del problema inicial.
Palabras clave: Clúster, centroides, algoritmos genéticos, heurísticos, nodos.
This paper tries to solve the well know Traveling Salesman Problem using clustering and genetic algorithms, so we divide a set of cities in clusters for minimize the number of cities when the genetic algorithm will be applied. Therefore we propose a new method to do the clusters, so we define K points and call it centroids. This points being clusters and we recalculate centroids so that the distance between cities and its centroids will be minimum until centroids do not change more. Then we applied the genetic algorithms on each cluster to minimize the tour´s length in each cluster. Finally we propose a method to unite all clusters minimizing the tour´s length final.
Keywords: Clusters, centroids, genetic algorithm, heuristic, nodes.
Los algoritmos genéticos (AG) han sido utilizados para resolver el Problema del Agente Viajero (PAV), sin embargo, el tiempo computacional para resolverlo crece a medida que aumenta el número de ciudades, a pesar de ello, estos heurísticos muestran resultados satisfactorios en tiempos computacionales menores en comparación a otros algoritmos utilizados para resolver este tipo de problemas. La Programación Entera, es el método en donde se han obtenido los mejores resultados, no obstante, la complejidad computacional sigue siendo una barrera.
Problemas relativamente pequeños del PAV han logrado obtener resultados muy cercanos al óptimo y frecuentemente lo han encontrado. En contra parte los problemas con grandes cantidades de nodos, 200 o más, muestran dificultad para su resolución.
Por lo anterior, en este trabajo de investigación se ha identificado que al dividir al PAV en subproblemas se podrían encontrar resultados satisfactorios en tiempos computacionales adecuados, como la industria lo requiere en la actualidad. Para ello, se vuelve necesario proponer un método que permita dividir al PAV en subproblemas o clústeres, de una forma eficiente, a través de la asignación de nodos representativos para cada conjunto de nodos llamados centroides; y mediante el cálculo iterativo se logre encontrar la distancia menor entre el centroide y sus respectivos nodos; de esta manera se pretende aplicar los AG sobre cada clúster en busca de la distancia más corta, y finalmente unir a todos los nodos en una ruta única, factible y mínima.
La propuesta del presente trabajo de investigación radica en la forma en que se busca hacer más eficiente a la clasificación de los nodos: a partir de reducir la distancia entre estos y los centroides, mediante el cálculo de estos últimos, aplicando la media aritmética; a diferencia de Tanasanne (2014) que lo hace con la distribución de probabilidad normal, lo que supone un mayor tiempo computacional.
El clúster del PAV es definido por Laporte (2002) como un gráfico completo G = (V,E) en el caso no dirigido o (V,A), en el caso dirigido donde V={v1,…,vn} es un conjunto de vértices dividido en m clústeres (V1,…,Vm). El conjunto E= {(vi, vj): vi, vj ∈ V, i < j} es un conjunto de uniones, y A= {(vi, vj): vi, vj ∈ V, i≠j} es un conjunto de arcos tal que ambos, los dirigidos y los no dirigidos, pueden considerarse. Una matriz de costos C= (cij) es definida sobre E o A.
El clúster del problema del agente viajero (CPAV) consiste en determinar el costo mínimo de un ciclo hamiltoniano o un circuito sobre G, en el cual los vértices de cualquier clúster VK son contiguos. El CPAV coincide con el PAV cuando todos los clústeres tienen un semifallo. En general el CPAV puede ser transformado rápidamente en un PAV, agregando una constante arbitraria M como costo dentro de cada clúster o médiate la resta de M desde los costos dentro del clúster. Sin embargo tal transformación presenta una cantidad justa de degeneración en el problema, y puede ser preferible para resolver el CPAV directamente mediante un algoritmo especializado.
Fue en el año de 1800 cuando el matemático irlandés William Rowand Hamilton (Mitchel, 1996), estudió por primera vez el PAV, al diseñar un juego entre dos competidores en un icosaedro. Este juego consiste en hacer un recorrido por los veinte puntos del icosaedro usando las conexiones de la figura e iniciando y terminando en el mismo punto sin repetir los lugares visitados.
El 5 de febrero de 1930, en un coloquio en Viena, el matemático austriaco Karl Menger mencionado por Applegate (2006) plantea por primera vez el PAV en lenguaje matemático. En 1931 Menger tuvo una estancia en Harvard donde dictó varios seminarios y en uno de ellos mencionó el problema de las rutas mínimas y el PAV. Whitney se interesó en el PAV, proponiendo encontrar la solución entre las 48 capitales de los estados en la parte continental de la Unión Americana, según Applegate (2006). Con este simple ejemplo inició la divulgación del PAV en los centros de investigación de la Unión Americana. El PAV ya había surgido desde 1759, en este problema se pretendía mover al caballo del juego de ajedrez en todas las posiciones exactamente una vez. En 1832 el alemán Voigt escribió un libro sobre como tener éxito al resolver el PAV (Zbigniew, 1994). Posteriormente, Homaifar (1992) propuso un enfoque en el cual se puede encontrar con certeza la solución óptima. El procedimiento consiste en la generación de todos los tours posibles en donde se evalúan sus correspondientes distancias. El tour con la distancia más pequeña es considerado como el mejor.
El PAV muestra todos los aspectos de optimización combinatoria. Durante la década de 1950, la programación lineal se estaba convirtiendo en una fuerza vital en la informática de soluciones a problemas de optimización combinatoria. Esto se debió a la financiación proporcionada por la Fuerza Aérea de los EE.UU y al interés de obtener soluciones óptimas, una de las razones por las cuales el PAV se encontraba en el interés de todos. Los intentos de resolver el PAV fueron inútiles hasta mediados de la década de 1950 cuando Dantzig et al. (1954) presentaron un método para resolver el PAV. Ellos mostraron la eficacia de su método de resolución de una instancia de 49 de las ciudades. Posteriormente, se hizo evidente a mediados de 1960, que el PAV no puede ser resuelto en tiempo polinomial usando técnicas de programación lineal, por lo que se plantea la complejidad computacional, lo que significa que cualquier esfuerzo programable para resolver problemas tales crecería de forma no polinomial con el tamaño del problema.
Estas categorías de problemas que se conoce como NP-completos. Existe un gran progreso en el tratamiento de problemas NP-completos, como el PAV. Se han encontrado soluciones a los casos de PAV con tamaños de entrada muy pequeños, debido a la complejidad de su solución. También algunas soluciones en tiempos polinomiales se han encontrado en casos especiales del PAV. Los investigadores incluso han recurrido a la búsqueda de algoritmos de aproximación polinomial para variaciones NP-completo del PAV mencionados en Dantzig et al. (1954). Hasta el día de hoy, una solución eficiente para el caso general PAV, o incluso a cualquiera de sus variantes NP-completos, no se ha encontrado.
William Cook (Cook, 2000) profesor de la Escuela Técnica Industrial e Ingeniería de Sistemas en Georgia es considerado el más avanzado en cuanto a resultados en el PAV según la comunidad científica. Cook puso en marcha su primer proyecto del PAV en 1988 cuando era profesor en la Universidad de Columbia en Nueva York junto con Vasek Chvátal un profesor de matemáticas de la Universidad de Rutgers. Más tarde los dos investigadores reclutaron a David Applegate universitario graduado de Carnegie Mellon, y a Robert Bixby, profesor de la Universidad Rice en Houston. En 1992, los cuatro encontraron la ruta óptima para 3 038 ciudades (Cook, 2000), con lo que rompieron el récord anterior de 2 392 ciudades (Cook, 2000) establecido en 1987 por Manfred Padberg, de la Universidad de Nueva York y Giovanni Rinaldi, del Instituto de Análisis de Sistemas y Ciencias de la Computación en Roma. La revista Discover considera a la solución de 3038 ciudades (Cook, 2000) como una de las 50 mejores historias de ciencia en 1992. Desde entonces este equipo ha recibido dicha mención en cinco ocasiones. Los investigadores resolvieron el PAV para 4 461 ciudades de Estados Unidos en 1993, 7 397 ciudades en 1994, 13 505 ciudades en 1998 y un tour en Alemania de 15 113 ciudades en el año 2001. En abril de 2004, que establece su registro actual con un recorrido óptimo de 24 978 ciudades suecas (Cook, 2000). Sin embargo no han especificado como trabaja su algoritmo.
En 1962, investigadores como Box, G.J. Friedman, W.W. Bledsoe y H.J. Bremermann mencionados en (Haupt, 1998) habían desarrollado independientemente algoritmos inspirados en la evolución para optimización de funciones y aprendizaje automático, pero sus trabajos generaron poca reacción. En 1965 surgió un desarrollo más exitoso, cuando Ingo Rechenberg mencionado en (Haupt, 1998), quien entonces trabajaba en la Universidad Técnica de Berlín, introdujo una técnica que llamó estrategia evolutiva, aunque no se parecía a los AG actuales. En esta técnica no había población ni cruzamiento un padre mutaba para producir un descendiente, y se conservaba el mejor de los dos, el cual se convertía en el padre de la siguiente ronda de mutación.
Chatterjee et al. (1996) propone un algoritmo genético con un plan de reproducción a través de la mutación para un operador evolutivo que puede ser directamente aplicado para una permutación de n números para una aproximación de la solución del PAV. El análisis de esquema del algoritmo muestra que una reproducción con operadores de mutación, preserva la propiedad de convergencia global de un algoritmo que establece el teorema fundamental de los algoritmos. En este algoritmo se evita un paso intermedio de codificación a través de las llaves que preservan el cruzamiento o permutación n usando un estado de ajuste, lo que hace que la propuesta sea interesante.
Según Buthainah (2008) La mejora continua en el valor del AG ha sido atractivo para muchos tipos de métodos de resolución de problemas de optimización, particularmente los AG trabajan muy bien en mezcla (discreto continuo) de problemas combinatorios; además son menos susceptibles a que los resultados obtenidos sean los mismos de una generación a otra. Sin embargo, tienden a ser computacionalmente caros. Una población inicial con genomas o cromosomas es generada aleatoriamente en poblaciones sucesivas, o generaciones, es obtenida mediante operadores genéticos como la selección, cruza y mutación para evolucionar las soluciones a fin de encontrar la mejor. El operador de selección escoge a dos miembros de la presente generación a fin de participar en las siguientes operaciones: cruza y mutación. El operador de cruza intercambia a los alelos de dos padres para obtener dos hijos. La mutación se crea en un corto periodo después del cruce, intercambiando alelos de forma aleatoria.
En nuestro grupo de trabajo se ha estudiado el problema de secuenciación de trabajos (PST) y su resolución a través del PAV mediante AG; en donde se propone una codificación del PST al del agente viajero. Se revisan las diferentes metodologías y enfoques utilizados para resolver el PAV para posteriormente proponer dos versiones de torneo en el algoritmo genético; el primero llamado determinístico y el segundo llamado aleatorio. Se realizan diferentes pruebas para la solución del PAV, utilizando ambos algoritmos bajo diferentes parámetros para los operadores de número de individuos, número de iteraciones a realizar, probabilidad de cruce y probabilidad de mutación; a partir de estos se obtienen los parámetros y el algoritmo adecuado a realizar. Posteriormente se realiza una decodificación para transformar al PST en un PAV en donde se experimenta la solución de este último en búsqueda de su optimización, para después volver a la codificación del PST. Se realizan diferentes experimentos tomados de la literatura para su comparación con los resultados obtenidos en los diferentes artículos.
Sivaraj et al. (2012) menciona que resolver un problema NP, como el problema del agente viajero (PAV) es uno de los mayores retos enfrentados por los analistas, incluso a través de múltiples técnicas que están disponibles. Diversas versiones de los algoritmos genéticos (AG) han sido presentadas por investigadores, con la intensión de mejorar su eficiencia en la solución del PAV. Los algoritmos genéticos con clústeres (CAG) fueron presentados recientemente y en su artículo Sivaraj et al. (2012) analiza los resultados obtenidos por la implementación del PAV. Se observa que CGA efectivamente encuentra la solución óptima, más pronto que los algoritmos genéticos estándar (SGA), en tres diferentes instancias consideradas. Propone también el diseño de los parámetros del CGA para el PAV. El esquema de codificación elegido es la permutación, en donde los genes dentro de los cromosomas representan el orden en el cual uno tiene que viajar desde la ciudad inicial. La idea aquí es que si existen n ciudades en el problema elegido, estos se han dividió en n/x subgrupos (clústeres) donde x representa el número de cromosomas en toda la población, y n representa el tamaño de los clústeres. El propósito del enfoque efectivamente busca localmente y combina el mejor resultado local desde una solución global. Todas las ciudades del problema son agrupadas en clústeres, usando K-clústeres, donde cada grupo tendrá una colección de ciudades (Figura 1). La selección de los padres, operadores como cruza o mutación son aplicados y el mejor ordenamiento de las ciudades dentro de cada grupo es calculado independientemente como se muestra en la figura 2 y finalmente los resultados desde cada grupo son combinados para formar una simple solución como se muestra en la figura número 3.
En lo referente a la implementación y resultados, se utiliza TSPLIB con las instancias br17, ftv44 y Kro124p. La condición de paro del algoritmo genético, es el número fijo de generaciones o hasta que converjan los cromosomas en los mismos valores por 5 generaciones consecutivas. Los experimentos son conducidos con dos planes.
En el primer plan, el algoritmo se ejecuta hasta que la solución converja (valores sin cambios durante 5 generaciones).
Los parámetros utilizados para los operadores son:
Laporte (2002) describe varias aplicaciones de los clústeres del problema del agente viajero (PAV) surgidas en áreas tan diversas como el enrutamiento de vehículos, manufactura, operaciones de la computadora, examinación de horarios, examen citológico, la integración de comprobación de circuitos.
Tanasanne (2014) propone métodos para resolver el PAV utilizando técnicas de clústeres y métodos evolucionarios. El modelo mixto gaussiano y K-clústeres, son dos técnicas de clústeres que se consideran en este artículo. Se forman clústeres para el problema del agente viajero ordenando grupos con los nodos más cercanos. Posteriormente se aplica el método evolucionario en cada clúster. Los resultados obtenidos con algoritmos genéticos y con colonia de hormigas son comparados. En los últimos pasos, se propone un método de conexión de clústeres para encontrar la ruta óptima entre cualquiera de dos clústeres. Estos métodos son implementados y probados en el (TSPLIB). Los resultados son comparados en términos de promedio de la mínima longitud del tour y el promedio del tiempo computacional. Los resultados demuestran que las técnicas de clústeres son capaces de mejorar la eficiencia de los métodos evolucionarios sobre el PAV. Por otra parte los métodos propuestos pueden ser aplicados en otros problemas.
Existen diferentes tipos de técnicas de clústeres como los basados en prototipos, basados en centros, basados en gráficos y basados en densidades (Tan, 2006).
Tanasanne (2014) plantea cada objeto en K-means clustering (la cual es la denominación que da a su algoritmo), puede ser asignado a uno de los clústeres; el método comienza decidiendo cuántos clústeres se utilizarán y se denotan por K. El valor de K generalmente es un valor entero pequeño. K nodos son seleccionados para ser los clústeres iniciales; estos nodos pueden ser seleccionados en cualquier forma, pero el método puede ser mejor, si K nodos son seleccionados lo más alejados posibles. Existen muchos caminos por los cuales los clústeres podrían potenciarse. Un método para medir la calidad de un conjunto de clústeres, es a través de la suma del cuadrado de las distancias entre cada nodo y el centroide del clúster al que pertenecen; este valor debe ser lo más pequeño posible.
Todos los nodos pueden ser asignados a un clúster por la selección de un centroide que proporcione la mínima distancia entre el nodo y el centroide. Posteriormente tenemos K clústeres basados en K centroides originales, pero el centroide podría no ser el verdadero de los clústeres, puesto que los centroides de cada clúster pueden ser recalculados. Cada nodo podría reasignarse al clúster que tenga el centroide más cercano al nodo. Este proceso puede repetirse hasta que el centroide no se mueva más.
Algoritmo K means:
Modelo Gaussiano Mixto propuesto por Tanasanne (2014) es una colección de K distribución gaussiana. Cada distribución representa un clústeres de puntos de datos. El modelo utiliza el algoritmo de esperanza y maximización (EM), para ajustar la distribución gaussiana de los datos. El Algoritmo inicia definiendo el número de clústeres (K) y eligiendo los paramentaros de K distribuciones gaussianas.
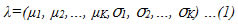
Cuando cada clúster tiene una distribución normal con N (µi, σi2).
Por otra parte, Tanasanne (2014) propone también el modelo gaussiano mixto; el cual es una colección de K distribución gaussiana. Cada distribución representa un clúster de puntos de datos. El modelo utiliza el algoritmo EM, para ajustar la distribución Gaussiana de los datos. El algoritmo inicia definiendo el número de clústeres K y eligiendo los paramentaros de K distribuciones gaussianas. Cuando cada clúster tiene una distribución normal con N (µi, σi2).
El algoritmo EM calcula la probabilidad que cada punto pertezca a cada distribución y utiliza estas probabilidades para calcular una nueva estimación para los parámetros. Estas iteraciones continúan hasta que las estimaciones de los parámetros ya no cambian o cambian muy poco.
El algoritmo EM consiste en lo siguiente:
El método propuesto para resolver el PAV mediante clústeres y AG; pretende minimizar las distancias del problema en cuestión de la siguiente manera:
El algoritmo a implementar presenta un menor número de operaciones al momento de calcular y recalcular a los centroides de cada clúster, a diferencia de lo que hace Tanasanne (2014), quien propone calcular los centroides mediante la minimización de distancias utilizando una distribución de probabilidad normal. Además, el método propuesto en esta investigación utiliza el valor de la media aritmética de los datos de ubicación de cada nodo en su clúster respectivo, lo que hace posible recalcular al centroide y encontrar si existe algún nodo de otro clúster que se encuentre más cercano al centroide en cuestión.
El algoritmo propuesto se programa en lenguaje MATLAB. En este momento la investigación en cuestión se encuentra en la fase de programación por lo que aún no se ha experimentado y es parte de actividades futuras para este proyecto.
Applegate, D. (2006) The traveling salesman problem: Computational study. Princeton University Press, USA.
Buthainah, F. (2008) Enhanced traveling salesman problem solving by genetic algorithm technique. World Academy of Science, Engineering and Technology, 38, 296-300.
Dantzig, G., Fulkerson R., Johnson, S. (1954) Solution of a large scale traveling salesman problem Journal of the Operations Research Society of America, 2(4), 393-410.
Chatterjee, S., Carrera, C., Lynch, L.A. (1996) Genetic algorithms and traveling salesman problem. European Journal of Operational Research, 93(3), 490-510.
Cook, S. (2000) The P versus NP Problem. Clay Mathematics Institute.
Haupt, E. (1998) Practical genetic algorithms. Wiley-Intersciencie Rewiew.
Homaifar, A. (1992) Schema analysis of the traveling salesman problem using genetic algorithms complex systems. Computer Engineering NC AT University, 6(6), 533-552.
Laporte, G. (2002) Some applications of the clustered travelling salesman problem. Journal of the Operational Research Society, (53), 972–976.
Mitchell, M. (1996) An introduction to genetic algorithms. Cambridge, Massachusetts London, England.
Sivaraj, R., Ravichandran, T., Priya, D. (2012) Solving traveling salesman problem using clustering genetic algorithm. International Journal on Computer Science and Engineering (IJCSE), 4, 1310 -1317. ISSN: 0975-3397.
Tan, P. (2006) Steinbach, M., Kumar, V. Introduction to data mining. Boston: Pearson Addison Wesley.
Tanasanne, P. (2014) Clustering evolutionary computation for solving travelling salesman problems International Journal of Advanced Computer Science and Information Technology (IJACSIT), 3, (3), 243-262, ISSN: 2296-1739
Zbigniew, M. (1994) Genetic algorithms data structures evolution programs. Springer, New York, USA.
[a] Gustavo Erick Anaya Fuentes estudió la Licenciatura en Ingeniería Industrial y la Maestría en Ciencias en Ingeniería Industrial en la Universidad Autónoma del Estado de Hidalgo; se desempeña como profesor Universitario en la misma Institución Educativa, apoyando a programas Educativos como Comercio Exterior, Ingeniería en Geología Ambiental, Ingeniería Civil e Ingeniería Industrial. En 2012 elaboró la Tesis titulada “El Problema del Agente Viajero resuelto con Algoritmos Genéticos: Un método para encontrar una solución al Problema de Secuenciación de Trabajos”, con el que obtuvo el grado de Maestro en Ciencias. Con el mismo título de investigación se redactó un artículo de investigación, el cual ya ha sido aceptado en la Revista de Informática Industrial de Elsevier.
[b] Eva Selene Hernández Gress egresó de la licenciatura en Ingeniería Industrial y de Sistemas en el Tecnológico de Monterrey Campus Hidalgo, realizó sus estudios de Maestría en Ciencias con Especialidad en Ingeniería Industrial en el Tecnológico de Monterrey Campus Estado de México y obtuvo el Doctorado en Ciencias en Ingeniería Industrial en la Universidad Autónoma del Estado de Hidalgo. Labora en la Universidad Autónoma del Estado de Hidalgo, donde es Profesor Investigador, es candidato del Sistema Nacional de Investigadores. Ha publicado 5 artículos en revistas indexadas en el Thompson Reuters y presentado más de diez ponencias en Congresos internacionales. Ha escrito 5 capítulos en libros.
[c] Joselito Medina Marín recibió el grado de Ingeniero en Computación por parte de la Universidad Autónoma de Guerrero en el año de 1997. En el 2002 recibió el grado de Maestro en Ciencias con especialidad en Computación, y en el 2005 el grado de Doctor en Ciencias con especialidad en Computación, ambos grados fueron otorgados por el Centro de Investigación y de Estudios Avanzados del Instituto Politécnico Nacional (CINVESTAV – IPN). Actualmente se encuentra laborando en el Área Académica de Ingeniería de la Universidad Autónoma del Estado de Hidalgo como Profesor-Investigador. Las líneas de investigación que cultiva incluyen teoría de Redes de Petri, bases de datos activas, simulación de eventos discretos y lenguajes de programación.
[*] ganaya@uaeh.edu.mx
[a] Universidad Autónoma del Estado de Hidalgo, Área Académica de Ingeniería, Carr. Pachuca- Tulancingo Km 4.5, Cd. Universitaria, Pachuca Hidalgo.
[b] Área Académica de Ingeniería, Instituto de Ciencias Básicas e Ingeniería, Universidad Autónoma del Estado de Hidalgo, Carr. Pachuca Tulancingo Km 4.5, Ciudad del Conocimiento, Col. Carboneras, C. P. 42184, Pachuca de Soto, Hgo., México.