Figura 1. Impacto de los diferentes métodos de surtimiento de las piezas en la frontera de la línea. Fuente: Veronique Limère, 2013. To kit or not to kit: optimizing part feeding in the automotive
El objetivo de cualquier organización es aumentar la productividad con menor costo. Para lograr esto se están buscando nuevas tecnologías y filosofías en los sistemas de Justo a Tiempo y Kan-Ban. El uso de sistemas de “Supermercado” es una evolución del Kan-Ban como una de las herramientas para lograr el Justo a Tiempo de la producción ya que busca reducir los inventarios en el proceso de producción. La implementación de estos sistemas mediante algoritmos genéticos hará más amplia su área de aplicación y estudio. Este trabajo presenta una resolución de los modelos de los estudios de Nils Boysen y Simon Emde mediante ese método con el objetivo de extender su área de estudio respecto al tema. Los resultados obtenidos en el estudio presentan dificultades en el proceso de simulación pero los resultados son favorables y similares a los de los que los autores presentan.
Palabras clave: Sistemas de supermercado, algoritmos genéticos, Kan-Ban, justo a tiempo.
The goal of any organization is to increase productivity in lower cost. To achieve this, new technologies and philosophies in JIT and Kan-Ban systems are being sought. The use of "Supermarket Systems" is an evolution of Kan-Ban as one of the tools to achieve JIT production as it seeks to reduce inventories in the production process. The implementation of these systems using genetic algorithms make it expands its area of application and study. This paper presents a resolution of a model of the studies from Nils Boysen and Simon Emde by this method with the aim of extending their area of study on the subject. The results of the study have difficulties in the simulation but they are favorable and similar to those authors presented by other authors.
Keywords: Supermarket Systems, Genetic Algorithms, Kan-Ban, JIT.
Los sistemas Kan-Ban se tratan de un sistema informativo que armoniosamente controla la producción necesaria de los productos en las cantidades necesarias y en el tiempo necesario, en cada proceso (Monden, 1983). El sistema Kan-Ban es una de las formas o elementos para gestionar el método de producción Justo a Tiempo (JIT). Sin embargo, a veces el montaje en las líneas tiene un proceso muy largo y la distancia desde el almacén hasta las estaciones es demasiado grande. En este caso, se utiliza otra estrategia en la que hay áreas de inventario dispersas, que se utilizan para alimentar las estaciones cerca de ellas. Por lo general, en la práctica, cada 20 a 30 estaciones se suministran por medio de un almacén descentralizado denominado “Supermercado” (Boysen y Bock 2011).
El concepto de surtimiento de materiales por medio de supermercados surge en la empresa automotriz Toyota, modelo inspirador y arquetipo del método Kan-Ban. La idea del supermercado surge gracias a Taiichi Ohno, quien con su famosa descripción de su inspiración para Kan-Ban al regresar de una visita a Estados Unidos, durante la década de 1950, en la que él queda más impresionado con el tipo de manejo de materiales que se llevaba en los supermercados, que con los modelos de manufactura de las empresas de Estados Unidos. La idea fue tener todos los bienes disponibles en todo momento, Ohno (1988) dice:
“Dentro del supermercado se nos ocurrió la idea de ver el proceso de la tienda como un tipo de línea de producción. El proceso posterior (cliente) va al proceso anterior (supermercado) para adquirir las piezas necesarias (productos) en el momento y en la cantidad necesaria. El proceso anterior inmediatamente produce la cantidad que acaba de tomar (realmacenamiento de las estanterías)” (p. 26).
El presente trabajo trata sobre lo referente a la aplicación básica de este concepto de surtimiento de materiales en las líneas de ensamble de las empresas, denominado Supermercado, pero implementado desde una manera totalmente diferente: una visión matemática con la aplicación de algoritmos genéticos (AG) para su resolución.
En la primera parte se explica de manera general en qué consisten y cuáles son los sistemas de suministro de materiales más comunes. Se comenta brevemente el inicio del sistema JIT y Kan Ban que son la pauta para la aplicación el sistema de Supermercado.
La segunda parte habla de manera generalizada respecto a la solución de problemas por medio de optimización matemática, en este punto se toma el interés e importancia sobre la resolución por medio de AG.
La tercera parte da referencia a la problemática del y la descripción del objeto de estudio, explicando punto por punto como es la relación de resolución de la implementación de AG con respecto al número óptimo de supermercados a implementar.
La última parte explica de manera breve la solución a dicho problema con el método propuesto y la comparación que se tiene con los resultados reportados. Se dan a conocer las conclusiones del estudio y sus futuras aportaciones.
La principal tarea de un buen método de suministro de materiales es surtir los materiales adecuados, en el momento adecuado, en el lugar adecuado y en la cantidad exacta a la línea de producción. Con el fin de ser competitivo en la industria, es importante que este proceso de suministro se ejecute de una manera rentable. Sin embargo, no solo el costo de suministro de las partes debe ser considerado, también el impacto en las operaciones de montaje debe ser evaluado.
Los diferentes sistemas de alimentación de la línea de producción tendrán una influencia en cómo se usarán las partes en la frontera de las estaciones. También es necesario considerar que el espacio disponible en la frontera de la línea que es muy limitado. (Limère, 2012). En la industria se pueden encontrar diferentes sistemas de suministro de materiales, Limère (2012), explica de manera general los diferentes tipos de surtimiento más utilizados en las industrias:
El método más sencillo y común es el de suministro de materiales a granel, almacenamiento general, de reposición continua o de almacenamiento en la línea. Bajo este sistema de almacenamiento, las partes se suministran a la planta de fabricación en grandes cantidades en un solo viaje dentro de un contenedor específico. Los contenedores se almacenan cerca de las estaciones de trabajo en la frontera de la línea, y un sistema de dos cajones o punto de reorden se utiliza para controlar la reposición. Este sistema es el más básico pero el peor para los fines de ahorrar desperdicios de espacio en la línea de producción.
El almacenamiento directo en la línea, causa que las piezas tengan primero que ser reempacadas de los grandes contenedores que llegan, en contenedores más pequeños antes de ser suministradas a la línea. Este sistema de suministro de materiales se denomina reducción.
Un tercer método de alimentación de línea es la secuenciación. La secuenciación de las partes significa que estas no se almacenan a granel en la frontera de la línea, pero sólo se suministran a la línea en el momento y en la cantidad que se necesitan según el esquema de montaje.
Por último, las piezas también se pueden agrupar en kits antes de que se suministren a la línea. El kit suministra una o más operaciones de montaje de un producto en la línea. Sobre todo en un ambiente de modelo mixto de alta varianza cada kit será diferente y los kits serán secuenciados según el programa de producción futuro. La cantidad exacta de los componentes necesarios se almacena en kits cerca de las estaciones de trabajo de montaje en la frontera de la línea y las reposiciones se llevan a cabo de acuerdo con el horario de montaje, que se basa en el ciclo de montaje o tiempo de procesamiento.
Los cuatro modelos arriba mencionados se pueden observar en la Figura 1 y son los sistemas de surtimiento más conocidos y usados en las industrias. Como se puede observar el sistema Kitting habla por sí mismo demostrando que es el que menos espacio ocupa, el que más lógica de suministro tiene y es el más flexible a los cambios que puedan surgir en la línea.
Figura 1. Impacto de los diferentes métodos de surtimiento de las piezas en la frontera de la línea. Fuente: Veronique Limère, 2013. To kit or not to kit: optimizing part feeding in the automotive
Surgimiento de sistemas JIT y Kan-Ban
Sistema de supermercado
Los supermercados son considerados como áreas de almacenamiento descentralizadas dispersas, que actúan como almacén intermedio para alimentar estaciones cercanas. Una de las ventajas de estos sistemas es la entrega rápida y frecuente de las piezas y de consolidación de carga al ser suministrada por carritos (Tow Trains). Sin embargo, los supermercados consumen espacio en el piso de la fábrica, que es escaso y caro (Emde y Boysen, 2012a)
El tipo de almacenaje habitual también puede causar estorbo al operador, quita demasiado espacio valioso en el taller y la peor razón es que se pierde el control total del material, una de las principales ventajas es evitar los grandes y estorbosos racks de la línea y el almacenamiento excesivo de partes.
Al ver que las secuencias de producción generalmente se conocen con suficiente antelación (entre tres y cuatro días en la industria automotriz), la lista de materiales determina exactamente cuántas partes se necesitan dentro de un determinado intervalo de tiempo en cada estación. Los sistemas clásicos de Kan-Ban según el Sistema de Producción Toyota (Monden, 1983) no aprovechan esta información, ya que solo surten el material que ya ha alcanzado un nivel crítico de stock ya definido. Sin embargo, a la espera de ser ''sorprendido'' por las bajas existencias, lo que podría requerir de entregas de emergencia si el próximo paro de línea programado en la estación no está demasiado próximo.
Esto es innecesario al conocer la información acerca del programa de la producción y la demanda de partes por estación, así como los plazos de entrega de material. Como consecuencia, al conocer estas condiciones se puede ejecutar sin problemas un sistema moderno y bien planificado de surtimiento basado en los supermercados (Golz, 2010).
La Figura 2 tomada de Emde y Boysen (2012a), muestra la distribución de una fábrica con dos supermercados. Donde se explica que el almacén central de recibo de materiales distribuye las partes en lotes considerablemente grandes a los supermercados en la línea, donde estos preparan el material para el surtimiento en la línea por medio de carritos o Tow Trains, los cuales rodean las estaciones correspondientes al área de surtimiento del supermercado. Estos autores comentan que el proceso delimitado de la distribución de las partes en la estaciones requiere de una ruta definida, una programación de entregas y la carga de materiales a remolcar en los trenes ya asignados al supermercado.
Si bien existen muchas maneras de estudiar y poner en marcha un supermercado, en la industria se tiene que empezar por lo básico: determinar el número de supermercados a implementar en la nave, lo que nos lleva también a su localización y a saber qué estaciones se van a surtir, este es el primer aporte de Nils Boysen y Simon Emde en sus estudios en cuanto a modelos matemáticos y el tema de estudio de este trabajo. Cada vez más estos autores van evolucionando sus estudios aportando hasta el momento modelos matemáticos para la distribución de las partes en la estaciones, definición de una ruta, una programación de entregas y la carga de materiales a remolcar en los trenes.
Figura 2.Un concepto de piso en la fábrica con dos supermercados Fuente: Emde y Boysen, (2012a)
Actualmente existe una mínima cantidad de información referente a la investigación de la implementación de supermercados, en tanto que hay demasiada sobre temas más generalizados como los son la filosofía de JIT y Kan-Ban. Lo anterior hace de este trabajo un tema poco estudiado a manera de investigación. Esto brinda la oportunidad para poder aportar resultados novedosos dentro de esta área.
Este trabajo propone una nueva metodología de solución para la optimización del modelo propuesto por Emde y Boysen (2012a) basada en AG para definir el número de supermercados a implementar en la nave, todo con base en la ubicación de las estaciones por coordenadas, la demanda de cada una de estas y el precio de implementación fijo por supermercado.
Los AG son algoritmos de optimización para maximizar o minimizar una función determinada, son algoritmos heurísticos adaptativos de búsqueda basada en las ideas evolutivas de selección y genética natural. Representan una explotación inteligente de una búsqueda al azar utilizado para resolver problemas de optimización (Sivaraj y Ravichandran, 2011).
Los AG simulan la supervivencia de los individuos más aptos entre todos los individuos de la población a través de generaciones sucesivas para resolver un problema. Cada generación se compone de una población de cadenas de caracteres que son análogas al cromosoma que se ve en el ADN. Cada individuo representa un punto en un espacio de búsqueda y una posible solución. Los individuos de la población entonces se hacen pasar por un proceso de evolución (Sivaraj y Ravichandran, 2011).
Los AG se basan en una analogía con la estructura genética y el comportamiento de los cromosomas dentro de una población de individuos con las siguientes bases: Los individuos en una población compiten por los recursos y parejas. Las personas más exitosas en cada "competencia" producen más descendencia que aquellos individuos que funcionan mal. Los genes de los individuos “buenos” se propagan por toda la población para que dos buenos padres puedan producir descendientes que son mejores que cualquiera de la combinación de los padres. Así, cada generación será más adecuada para su entorno (Goldberg, 2003).
Un parámetro crítico de los AG es la presión de seleccionar el proceso de selección de los mejores individuos entre toda la población para la próxima generación. Si se escogen individuos con genes “malos”, entonces la tasa de convergencia hacia la solución óptima es muy baja. Si se escogen individuos con genes “buenos”, entonces la tasa de convergencia hacia la solución probablemente sea atrapada en un rango óptimo debido a la diversidad de población. Por lo tanto, los métodos de selección en la población controlan la precisión, que a su vez determina la rapidez con la cobertura de algoritmos. La velocidad de convergencia de los diferentes esquemas de selección se estudió primero por Goldberg y Deb en 1990. El mecanismo de selección debe ser elegido de tal manera que se aproxime a la solución óptima global sin ser atrapado en el óptimo local. También debe abarcar el conocimiento de los datos existentes (Sivaraj y Ravichandran, 2011).
El presente trabajo buscará poder resolver el problema arriba mencionado de una manera más rápida y con un alcance mucho mayor al propuesto por los creadores del modelo, los cuales utilizan un modelo de programación dinámica por computadora para resolverlo contra el propuesto por algoritmos genéticos para demostrarlo.
Los Sistemas de Supermercados a pesar de ser un método de surtimiento conocido y muy sencillo de aplicar, que además se relaciona con sistemas de Kan-Ban y JIT, es un tema poco estudiado, donde existe escaso desarrollo de modelos matemáticos. Limère (2012) da una explicación clara sobre lo que sucede actualmente en las empresas:
Existen demasiados sistemas de suministro de materiales que se encuentran en la práctica, y cada uno de ellos ofrece ciertos beneficios operativos y desventajas. Sin embargo, se ha llevado a cabo poca investigación para profundizar en los diferentes métodos de suministro de materiales y el equilibrio entre ellos. Las decisiones de las empresas se basan principalmente en la intuición y la experiencia pero no existe conocimiento objetivo acerca de las ventajas y desventajas de los diferentes sistemas (p. 35).
Los estudios de Nils Boysen y Simon Emde profundizan sus investigaciones respecto al tema de los supermercados en los siguientes artículos:
Se elegirá por temas de conveniencia para el inicio de estudios de este trabajo, estudiar y resolver el tema número uno de los cinco artículos arriba citados, al ser el inicio de la investigación de los autores y principalmente ser el tema para implementar desde cero un supermercado, ya que los demás temas profundizan el contenido ya sobre temas que relacionan a supermercados ya puestos en marcha.
Descripción del objeto de estudio
En los sistemas de producción de hoy en día, la siempre creciente variedad de productos posee un gran reto para los sistemas de logística internos usados para alimentar las líneas de ensamble con las partes necesarias. Como respuesta a este reto muchos manufactureros, especialmente de la industria automotriz han definido el concepto de Supermercado como parte de una promesa para una estrategia para permitir entregas flexibles de pequeños lotes de material a un costo bajo (Emde y Boysen, 2012a).
Un reto importante dentro de este contexto es el de alimentar las partes a las unidades productivas (estaciones) en la línea de producción. De un lado, los materiales y las partes deben siempre buscar a las estaciones de trabajo a tiempo para evitar costos excesivos a causa de los paros de línea. Del otro lado, almacenamientos excesivos en las estaciones y/o el tránsito de la línea en el taller permite un costo elevado en el manejo y manutención de este material. De acuerdo al principio del JIT, una cantidad considerable de fabricantes están adoptando el tan llamado concepto de Supermercado. (Emde y Boysen, 2012a).
Un problema importante de optimización a considerar es la determinación del número y el lugar de instalación de las áreas de los supermercados. La implementación de supermercados conlleva un costo para poderlo poner en marcha, si se piensa en crear un gran número de supermercados, implicara muchos más costos que beneficios. Tener muy pocos, implica una mala ubicación, por otro lado, disminuirá en gran medida sus efectos positivos, por lo que, en el peor de los casos, es mejor mantener los sistemas tradicionales centralizados de almacenamiento. Utilizando el espacio disponible lo mejor posible al seleccionar el número óptimo de supermercados y su estratégica localización son de importancia crítica (Emde y Boysen, 2012a). En este trabajo se presenta un esquema de para resolver este problema de manera más óptima que los propios autores con los métodos de solución de algoritmos genéticos en vez de programación polinomial dinámica en el tiempo utilizada por ellos.
Del lado negativo, los supermercados consumen espacio en el piso de la fábrica, que es escaso y caro. Las piezas son guardadas en estantes diseñados para facilitar el acceso, de tal manera que los trabajadores puedan tomar las piezas de una manera cómoda, de manera análoga a los clientes de un supermercado tradicional, y por lo tanto suelen ser menos eficiente con el espacio de los almacenes tradicionales. Una implementación efectiva del concepto de supermercado también requiere de una inversión en equipos, personal y mantenimiento. Encontrar el mejor trabajo respecto a esta disyuntiva y la investigación de los beneficios operativos de los supermercados son cuestiones importantes que este trabajo abordará.
Acorde a Simon Emde y Nils Boysen, la planificación y el control de este concepto de logística interna, asciende al concepto de una tarea compleja que involucra varios problemas de decisión relacionados entre sí:
En este modelo se propone el inicio de la implementación de los sistemas de supermercados tomando el primer punto de los arriba mencionados y será estudiado con el primer modelo matemático propuesto por Simon Emde y Nils Boysen, en 2012 en su artículo Optimally locating in-house logistics areas to facilitate JIT-supply of mixed-model assembly lines, el cual trata el tema del número óptimo de supermercados a implementar, solución que conlleva también a saber su ubicación en la nave y las estaciones que va a suministrar.
Diseño teórico de la propuesta
Refiriéndonos al objetivo de la optimización, minimizar la suma de distancias ponderadas de cada supermercado a las estaciones que surte, regularmente es usado el problema de localización en el plano o Lay-Out, este es ciertamente aplicable, si se conocen las peculiaridades de transporte de los carritos en el surtimiento (Emde y Boysen 2012a). Los carritos Tugger usualmente no visitan a todas las estaciones de manera individual, sino que viajan en rutas predeterminadas con múltiples paradas.
Como la ruta del supermercado hacia las estaciones no es una línea recta, entonces cuando calculamos las distancias, debemos considerar la manera en que los carros Tuggers van a viajar: primero, desde el supermercado a la primera estación de trabajo a la que van a surtir en su ruta, después de estación a estación y finalmente, de regreso al supermercado a volver a llenar los carritos para volverlos a surtir. Aun así minimizar las distancias no necesariamente garantizan la mejor solución. Esto debido a que los Tugger tienen una capacidad limitada de cuantas y que estaciones puede surtir en un recorrido desentendiendo del consumo de partes en esas estaciones.
Las estaciones con menor demanda pueden ser una ruta, ya que los carritos no podrán ser capaces de servir a todas las estaciones por igual. Los supermercados saturados tendrán que usar carritos, rutas y stocks de seguridad adicionales, lo que conlleva un mayor costo de operación. Por lo tanto las distancias deberán de ser ponderadas por la demanda total de las estaciones surtidas por cada supermercado. La cantidad de partes exactas a surtir son determinadas por el consumo de ellas en el turno una vez que se conoce la secuencia.
Independientemente la demanda de los bines por estación o turno puede ser estimada con cierta precisión, como esto no requiere de un conocimiento muy profundo de la sincronización y composición de la secuencia del modelo sino una evaluación del promedio del volumen de producción. Finalmente como tercer componente, se fija un costo de creación y manutención de los supermercados. Tomando todos estos puntos en consideración, se usa la notación siguiente y definimos el problema de localización del supermercado como sigue:
Asumiendo una línea de montaje de modelo mixto clásico, a lo largo de los cuales hay s=1,..., S estaciones de trabajo, que tienen que ser suministradas con ds contenedores de partes del supermercado. La posición de cada estación en el Lay-Out de la fábrica se identifica por dos dimensiones de coordenadas (as, bs), que define la posición de ubicación de un Tugger o remolques (los que jalan a los carritos de supermercados o Tow Trains para su cambio en la línea) para el suministro de la estación de s. Con estas coordenadas, las distancias entre la estación es s y s+1, así como las distancias de zis entre la estación s y el supermercado i, donde i = 1,..., n, para ser cubierto por un Tugger al visitar estos lugares, se puede calcular fácilmente. Se deben de tomar en cuenta las siguientes consideraciones:
La notación utilizada en las ecuaciones es la siguiente
s - Estaciones de trabajo (s = 1 . . . S)
n - Variable para el número de supermercados a implementar (i=1…., n)
Ƭ - Precio fijo por supermercado a implementar
ds - Número de bins o contenedores del supermercado
as - Coordenadas en X de la posición de las estaciones de trabajo
bs - Coordenadas en Y de la posición de las estaciones de trabajo
es - Distancia entre estaciones s y s+1
zis - Distancia entre estación s y el supermercado i (i = 1 . . . n)
xi - Variable asignada para la primera estación a surtirse en el supermercado i a la estación s.
Dada s = 1,..., S estaciones de trabajo consecutivas a un suministro de partes del supermercado, el problema de ubicación del supermercado consiste en dividir las estaciones en un número variable de n = 1,..., S subconjuntos disjuntos, cada uno atendida por un supermercado diferente. Una solución se codifica como un vector X(n)={1,x2,x3,…,xn,S+1} → {2,…,S}, donde xi representa a la estación más a la izquierda del suministro del supermercado, en consecuencia, la estación más a la derecha servida por el supermercado i se determina por xi+1-1. Puesto que todas las estaciones se deben incluir en el área de surtimiento de algún supermercado, la estación más a la izquierda del primer supermercado siempre es 1, y la última estación más a la derecha es siempre S.
El vector es de longitud n+1 y sus miembros son configurados hacia el objetivo (1) de reducirse al mínimo y las limitaciones (2) y (3) se observan:
Minimizar F(X(n))
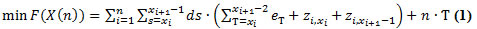
Sujeto a:
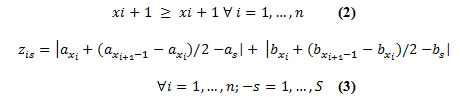
La función objetivo (1) tiene como finalidad reducir al mínimo el número de los supermercados n ponderado por su costo fijo Ƭ y la suma sobre todos los supermercados de la demanda total en las estaciones de los respectivos suministros de estos supermercados multiplicado por la longitud su ruta a través de las estaciones y su regreso. Hay que tener en cuenta el cálculo de las distancias que simula la ruta de un tren de remolque que tendrá que salir del supermercado: En primer lugar, la distancia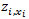 
del supermercado i a la primera estación xi en su zona de suministro, después la distancia 
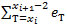de una estación a otra, y finalmente, la distancia 
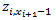al volver al supermercado.
Se debe considerar también que el área suministrada de la línea por un supermercado puede seguir cualquier tipo de camino, ya sea lineal o serpentinamente, esto puede ser codificado en la distancia entre las estaciones eT. La restricción (2) asegura que no hay zonas de abastecimiento traslapadas y la restricción (3) ayuda a calcular la distancia de cada supermercado para cada estación. Teniendo en cuenta que los pisos de la fábrica se caracterizan por líneas de conducción del lado de línea y curvas cerradas, la métrica Manhattan (o rectilínea) es método más adecuado para medir estas distancias. Los supermercados están colocados en medio de los dos puntos extremos de su área de surtimiento, ya que los Tuggers tendrán que comenzar su recorrido al salir del supermercado y finalmente acabarlo mediante su retorno nuevamente a él, probablemente desde el otro extremo de la zona de alimentación del supermercado. Además se debe considerar que, en muchos casos, los supermercados pueden, por supuesto, no encontrarse exactamente en el medio de las dos estaciones debido a que el ensamble en la línea de producción puede presentar un desplazamiento constante que no es idéntico en todas partes, esto no tiene que ser modelado explícitamente.
Un problema práctico que pueda surgir cuando se utiliza la función objetivo anterior es causada por la inclusión de dos factores de costo muy diferentes en una función objetivo común: Por un lado, el término que estima el costo futuro de operación y trata de minimizar las distancias y demandas en las áreas de suministro de todos los supermercados, los cuales tienden a ser menores mientras más supermercados existan. Por otra parte, el costo de implementación y de mantenimiento inferido mediante la creación de nuevos supermercados. Si bien el compromiso entre estos dos factores sin duda existe, estableciendo un costo exacto coeficiente Ƭ puede ser difícil en la práctica. Por lo tanto, propondremos un algoritmo en la siguiente sección que calcula todos los pares no dominados de estimación de costos de operación y el recuento de supermercado n. Todas estas soluciones son óptimas para su respectiva n.
Para cada supermercado i, la estación xi más a la izquierda en su zona de suministro debe ser determinada. Esto ajusta automáticamente la estación más derecha del área del supermercado precedente como xi-1. Dado que los conjuntos de estaciones ordenadas suministrados por cada supermercado no se pueden traslapar y los valores de distancia y demanda dependen sólo de la zona del supermercado al que pertenecen y no en los que vienen antes o después, las soluciones óptimas pueden ser eficientemente construidas por un enfoque de programación.
Sea k la primera estación en el área de un supermercado, G(k) el costo mínimo para el intervalo de la estación desde 1 hasta k-1 con G(1):= 0, f(j,k) el valor objetivo para el supermercado que sirve la estación j hasta k-1, determinado por:
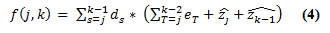
Donde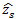 
es calculado con la ecuación (3) (con xi=j y xi+1=k). La programación es definida como:
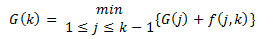
Ahora el objetivo es hallar el camino hacia S + 1 con el G(S+1) para un número dado n de supermercados. Una descripción formal del procedimiento es el cálculo de la frontera de todos los valores pares no dominados (n, pn, Gn(S+1)), (donde n es el número total de supermercados, pn codifica la correspondiente solución óptima, que puede ser decodificada por una sencilla recuperación hacia atrás, y Gn(S+1), es el valor de la función objetivo asociada con la solución).
Para saber interpretar la solución, se tiene que entender que se está creando una estación fantasma en las notaciones de la formula (S+1). Esto con el objetivo de poder interpretar a que estaciones va a poder surtir material cada supermercado, teniendo en cuenta la condición que se explica en este punto.
Ahora que se tiene toda la notación matemática para programar se explicará brevemente como es que fue resuelto este problema mediante algoritmos genéticos:
Se realiza una matriz de vectores ruta aleatorios con el programa anterior, este contiene el mismo número de estaciones (columnas) y un número introducido manualmente de individuos a cruzar (filas).
La matriz de vectores ruta aleatorios se resuelve y se acomoda ascendentemente por medio de sus costos finales. Solo se queda con la mejor mitad de resultados para cruzarlos, lo demás se desecha.
Para el cruce se sigue el procedimiento normal de un algoritmo genético. Se genera una matriz aleatoria con valores entre 1 y el número de individuos / 2, de 2 columnas y el número de individuos / 4 filas que nos rige como combinar los vectores. Se determina la posición de los vectores a cruzar de manera aleatoria, esta posición no puede cambiar el primer ni el último valor del vector, ya que es el mismo para todos.
Al momento de hacer el cruce y se generen los nuevos vectores en la matriz, se puede dar el caso en que se tengan valores repetidos. En estas circunstancias se tienen que desechar los valores repetidos y agregarle valores nuevos a dicho vector, los valores nuevos tienen que ser valores que no pasen del número total de estaciones +1 que se tienen en el problema. El vector tiene que ser llenado con los valores que no aparecen seleccionándolos aleatoriamente de una población de valores que no contiene el vector, acomodado dicho vector ascendentemente nuevamente.
Para la mutación se genera un valor aleatorio entre el 0 y el 1, dicho valor se compara con un índice de mutación que se introduce manualmente en el problema y si este es menor a dicho índice se procede a mutar el valor. Se debe de considerar que el primer y el último valor del vector no se pueden cambiar, solo los valores intermedios. Para esto antes de generar la mutación se deben de conocer los valores que no tiene vector y así en el caso de que tenga que mutarse se puede elegir uno de esos valores aleatoriamente para agregarlo al vector y volverlo a acomodar ascendentemente.
Los nuevos valores de la matriz son resueltos nuevamente y se vuelven a acomodar ascendentemente, quedándonos con el primer vector y su valor solución de la matriz, dejándolo como el mejor de la población.
Se genera un ciclo para todo este procedimiento, con un número de iteraciones para los valores desde 1 hasta el total de estaciones. Los mejores resultados para cada caso se guardan en una matriz alterna y al final del ciclo esta matriz es ordenada ascendentemente eligiendo al primer vector y su valor final como solución del problema.
Para poner a prueba el método de algoritmos genéticos anteriormente mencionado se resolvió un problema que presentan los autores en su artículo para su comparación, los datos se presentan en la siguiente tabla:
Tabla 1. Datos del Ejemplo
Solo se presentan los datos de las coordenadas y las demandas de cada estación, para este ejemplo se maneja un Ƭ = $300 por implementación de Supermercado. Los autores manejan los siguientes costos en como los más óptimos dependiendo del número de supermercados a implementar:
Tabla 2. Resultados óptimos para el problema presentado en Emde et al., (2012)
La ruta de surtimiento queda de la siguiente manera según dichos resultados del autor:
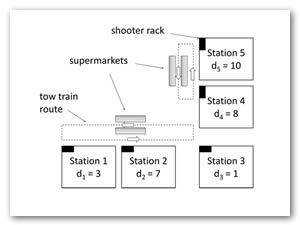
Figura 3. Ruta de surtimiento óptima para el problema de los autores
Fuente: Simon Emde y Boysen (2012a).
Resolviendo el problema con el algoritmo genético encontramos los siguientes resultados:
Figura 4. Resultados obtenidos con el algoritmo genético
La primera parte de la Figura 4 muestra el costo mínimo de todas las posibilidades de solución del problema que se encontraron en las iteraciones, la segunda parte muestra un vector que da a conocer la ruta con la que se obtuvo ese valor. Con esto podemos concluir que los resultados son los mismos a los expuestos por los autores, por lo que la propuesta de resolución por medio de algoritmos genéticos se puede concluir como aprobatoria.
En la Figura 5 se muestra el comportamiento de la resolución del algoritmo genético al momento de optimizar en un ciclo de 10 iteraciones, mostrando así que los resultados van disminuyendo (mejorando) hasta llegar al nivel más óptimo dentro del ciclo de iteraciones del problema.
Figura 5. Comportamiento de resolución del problema con algoritmos genéticos
En este caso el ejemplo es muy pequeño y se puede resolver de manera simple, este punto se refiere a que llega al valor óptimo con pocas iteraciones. Lo siguiente es compararlo con problemas más grandes propuestos por el autor en su artículo y verificar que método tiene una mejor área de solución óptima dentro de su simulación para determinar si existe un mejor método o simplemente son similares.
El problema es similar al de una ruta crítica o un agente viajero, tiene características que lo hacen propio y único como lo son que la ruta tiene que ir en orden ascendente y no puede repetir números, el valor inicial de la ruta siempre debe de ser 1 y el valor final del vector siempre debe de ser igual al número de estaciones que se tienen. Estas circunstancias hacen que la simulación se torne interesante y a su vez la complique en cuestión del tiempo de resolución como se vio en el estudio.
Al expandir la visión del problema y dejar las plantas de producción, este podría aplicar para la localización de centros de distribución o plantas de producción, siempre y cuando las características arriba mencionadas se ajusten a las del problema.
Este estudio abre más el panorama sobre la situación actual de la implementación de los supermercados, ya que existe muy poco sustento matemático para su resolución. Desde un inicio se pretendió ese objetivo ya que existe poca información respecto al tema.
Con las pocas pruebas que se lograron realizar en el proceso de programación por algoritmos matemáticos y compararlas con las del autor con programación dinámica, podríamos concluir que las dos son muy similares en cuanto al área de resolución óptima (costo). Al final el problema se resuelve desde una alternativa totalmente distinta llegando a los mismos niveles de resultados óptimos.
Como arriba se menciona actualmente se está trabajando con la simulación de los resultados que maneja el autor para implementarlos en esta resolución y así poderlos comparar desde el mismo contexto.
Como no hay datos de las pruebas establecidas, se generaron los casos utilizados en nuestro estudio computacional, tal como las maneja el autor. Los datos que se deben de generar son solo tres:
Para la demanda ds se define un número al azar de manera uniforme en el intervalo [1; 100] para cada estación.
Para las coordenadas en la posición as se maneja que as=as-1+rndu(1,6), ∀s=2,...,S, donde rndu(1,6) significa un número entero dibujado aleatoriamente del intervalo [1; 6] iniciando con a1:=1.
Para las coordenadas en la posición bs se manejan todas como 1, bs queda fijo en 1 ∀s=1,...,S, por simplicidad de las resoluciones.
Para efectos de simulación el autor maneja diferentes valores del total de supermercado S y diferentes valores del costo de implementación T:
S = [10, 30, 60, 100, 150, 200, 300]
T = [500, 1000, 5000, 10000, 25000, 50000]
Con estos datos se necesita una simulación completa para comparar los dos métodos de solución respecto al tiempo de resolución, al área de costo óptima de resolución y a los límites de variables de entrada posibles del problema. Es necesario correr una simulación completa para comparar las matrices promedio y verificar los resultados.
También se planean definir diferentes casos con las variables del problema para encontrar un punto óptimo de combinación en el área de solución deseada (costo). Este punto se refiere a la experimentación, cambiando las probabilidades de mutación y el número de iteraciones, para definir que combinación es la mejor sin afectar el área de costo mínimo y aumentar demasiado el tiempo de simulación.
Battini, D., Boysen, N., Emde, S. (2013) Just-in-Time supermarkets for part supply in the automobile industry. Journal of Managment Control, 24, 209–212
Boysen, N., Bock, S., (2011) Scheduling just-in-time part supply for mixed-model assembly lines. European Journal of Operational Research 211, 15–25.
Emde, S., Boysen, N. (2012a) Optimally locating in-house logistics areas to facilitate JIT-supply of mixed-model assembly lines. International Journal of.Production Economics 135, 393–402.
Emde, S., Boysen, N. (2012b) Optimally routing and scheduling tow trains for JIT-supply of mixed-model assembly lines. European Journal of Operational Research, 212, 282–299.
Boysen, N., Emde, S. (2013) Scheduling the part supply of mixed‐model assembly lines in line‐integrated supermarkets. European Journal of Operational Research, 239(3), 820–829.
Goldberg, D.E. (2003) Genetic algorithms in search, optimization, and machine learning. Addison-Wesley Longman, Boston, MA.
Golz, G. G. (2010) Part feeding at high-variant mixed-model assembly lines. In. Proceedings of the 12th International Annual EurOMA Conference.
Limère, V. (2013) To kit or not to kit: optimizing part feeding in the automotive assembly industry. SPRINGERLINK, 11(1), 92–98.
Monden, Y. (1983) Toyota Production Systems: Practical approach to production management, Industrial Engineering and Management Press, Atlanta, GA.
Ohno, T. (1988) Toyota Production system: Beyond large-scale production, Productivity Press, Cambridge, MA.
Sivaraj, R., Ravichandran, T. (2011) A review of selection methods in genetic algorithm. International Journal of Engineering Science and Technology, 3(5), 3792–3797.
[a] José Roberto Valencia Vera es ingeniero industrial egresado del Instituto Tecnológico de Pachuca en 2011, estudiante de la Maestría en Ciencias de Ingeniería Industrial (2013-2014). Universidad Autónoma del Estado de Hidalgo, México, Instituto de Ciencias Básicas e Ingeniería, Área Académica de Ingeniería. Correo electrónico: robertovalenciavera@gmail.com
[b] Juan Carlos Seck Tuoh Mora, recibió los grados de Maestría y Doctorado en Ciencias en Ingeniería Eléctrica opción Computación por parte del Centro de Investigación y de Estudios Avanzados del Instituto del Politécnico Nacional en México, D.F., en 1999 y 2002 respectivamente. Actualmente es Profesor Investigador del Centro de Investigación Avanzada en Ingeniería Industrial en la Universidad Autónoma del Estado de Hidalgo, México. Sus intereses de investigación incluyen teoría de autómatas celulares y sus aplicaciones, computación evolutiva y simulación.
[c] Joselito Medina Marín, recibió el grado de Ingeniero en Computación por parte de la Universidad Autónoma de Guerrero en el año de 1997. En el 2002 recibió el grado de Maestro en Ciencias con especialidad en Computación, y en el 2005 el grado de Doctor en Ciencias con especialidad en Computación, ambos grados fueron otorgados por el Centro de Investigación y de Estudios Avanzados del Instituto Politécnico Nacional (CINVESTAV – IPN). Actualmente se encuentra laborando en el Área Académica de Ingeniería de la Universidad Autónoma del Estado de Hidalgo como Profesor-Investigador. Las líneas de investigación que cultiva incluyen teoría de Redes de Petri, bases de datos activas, simulación de eventos discretos y lenguajes de programación.