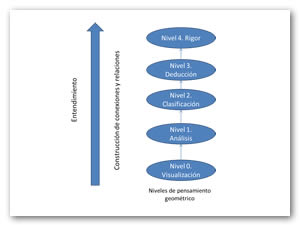
Figura 1. Niveles de pensamiento geométrico y su relación con el entendimiento.
En este artículo se presentan los elementos centrales de la teoría de van Hiele, la cual es útil para analizar el desarrollo cognitivo de los estudiantes al aprender geometría. Se describen cinco niveles de pensamiento por los que se transita durante el aprendizaje de la geometría, así como las fases de enseñanza necesarias para que los estudiantes logren un entendimiento conceptual de las ideas geométricas. Se resalta el hecho de que esta teoría permite explicar por qué los estudiantes muestran diversas dificultades de comprensión, además de aportar elementos útiles para diseñar escenarios de instrucción que favorezcan el desarrollo de procesos cognitivos de alto nivel.
Palabras clave: entendimiento, razonamiento, geometría, aprendizaje, niveles de van hiele
In this article we describe the key elements of the van Hiele theory, which is useful for analyzing the process of students' cognitive growth. Particularly we expose the characteristics of each one of five levels of thinking that students grow through in acquiring competence and understanding of geometrical ideas, and the teaching phases that assist students to move through the levels. The van Hiele theory is useful to explain why students show several difficulties to understand geometry, and provides useful suggestions to design learning scenarios that can favor development of high-level cognitive processes.
Keywords: understanding, reasoning, geometry, learning, van Hiele levels
La teoría de van Hiele describe el proceso de crecimiento cognitivo de los estudiantes al aprender geometría plana. Fue propuesta por Pierre van Hiele y su esposa Dina van Hiele-Geldof, en la década de los años cincuenta del siglo XX, y refinada por Pierre van Hiele en el libro Structure and Insight, publicado en 1986 (Pegg, 2014). Esta teoría constituye una herramienta útil para analizar el proceso de aprendizaje de la geometría; particularmente permite explicar por qué los estudiantes tienen dificultades para desarrollar procesos cognitivos de alto nivel, como aquellos que se llevan a cabo al elaborar demostraciones.
El cuerpo de la teoría lo integran dos componentes principales, la primera de ellas es una descripción de las diferentes formas de razonamiento o pensamiento que llevan a cabo los estudiantes, las cuales van desde el razonamiento intuitivo hasta el razonamiento formal y abstracto. Los autores consideran que existen diferentes niveles o etapas de entendimiento de las ideas geométricas y, por esta razón, como parte de la teoría, describen las características de cada uno de estos niveles. La segunda componente es una descripción de las características de cada fase o etapa del proceso de instrucción que puede ayudar a los estudiantes a alcanzar un nivel de pensamiento o razonamiento superior al que poseen en un momento dado (Guillén-Soler, 2004).
En relación con el avance entre niveles, la teoría establece que el logro de una nueva etapa de comprensión no puede llevarse a cabo a través de la enseñanza de hechos y procedimientos, sino que, el profesor debe crear un escenario favorable para que los estudiantes alcancen un nivel mayor de comprensión mediante una elección adecuada de problemas, es decir tareas que represente un reto intelectual más que dificultades procedimentales o de cálculo (van Hiele, 1999). En este enunciado, implícitamente se expresa que la comprensión de los estudiantes será mayor entre más diverso sea el tipo de problemas a los que se enfrentan en el aula.
De acuerdo con van Hiele, los niveles de pensamiento geométrico son progresivos y jerarquizados, esto significa que no se puede alcanzar un nivel si no se ha completado el nivel previo (Fuys, Geddes y Tischler, 1988). Completar un determinado nivel significa ser capaz de desarrollar los procesos de razonamiento que caracterizan a éste nivel. Por su parte, el aprendizaje de la geometría requiere de transitar por cada uno de los niveles en el orden establecido (Gutiérrez y Jaime, 1998) mediante la construcción de relaciones o conexiones significativas entre un nuevo conocimiento y los conocimientos previos que posee un estudiante (Figura 1). La teoría considera que cada uno de los niveles de pensamiento geométrico tiene sus propios símbolos lingüísticos y su propia red de relaciones que conectan esos símbolos; por ello, cuando existen diferencias de niveles en el proceso de comunicación entre dos personas, pueden surgir dificultades de entendimiento. Así, existen problemas para comprender las ideas geométricas, porque los profesores consideran que los estudiantes ya poseen ciertos conocimientos previos y un nivel de razonamiento que les permitirán entender nuevos conceptos; sin embargo, la realidad es que el nivel de pensamiento geométrico en el que se encuentran los estudiantes, generalmente es inferior al supuesto (Usiskin, 1982). Cabe resaltar que la teoría de van Hiele se enfoca a proporcionar elementos para apoyar la actividad docente. Es decir, sugerencias para diseñar escenarios que favorecen el desarrollo de entendimiento de las ideas geométricas, resaltando la importancia del lenguaje como medio para avanzar entre los diferentes niveles.
Nivel 1: Visualización o Reconocimiento. Los estudiantes reconocen a las figuras por su apariencia, sin que las propiedades de éstas jueguen un papel explícito en la identificación. El proceso de razonamiento sobre objetos matemáticos básicos (formas o figuras simples) se lleva a cabo mediante consideraciones visuales de los objetos como un todo (Burger y Shaughnessy, 1986). Las figuras geométricas tales como cuadrados, triángulos, rectángulos, circunferencias, se perciben en su totalidad como una unidad, sin diferenciar sus propiedades y componentes. Así, las propiedades de los objetos no juegan un papel explícito, para los estudiantes que se ubican en este nivel, en el reconocimiento de las formas geométricas.
Las representaciones de los objetos se identifican, comparan y operan con base en su apariencia física mediante descripciones visuales. Los estudiantes identifican a un rectángulo porque “parece una puerta” o la “tapa de una caja” (van Hiele, 1999), pero no porque tiene dos pares de lados paralelos y cuatro ángulos rectos. Los estudiantes que se encuentran en este nivel son capaces de distinguir, mediante la visualización, entre un cuadrado y un rectángulo; además, pueden reproducir figuras conocidas (Crowley, 1987). En algunos casos los estudiantes utilizan terminología geométrica, pero los términos utilizados tienen más un referente visual que conceptual. Al describir un rectángulo, se pueden utilizar la palabra “perpendicular” para un lado, sin embargo el término se utiliza con el significado de “vertical”. Los estudiantes son capaces de identificar algunas propiedades o características de las figuras, tales como el número de lados, sin embargo no pueden utilizar definiciones geométricas, sino que describen los atributos físicos de los dibujos que observan mediante expresiones como: “es redondo” o “es más largo que ancho” (Gutiérrez y Jaime, 1998).
Nivel 2: Análisis. Los estudiantes identifican una figura mediante sus propiedades, las cuales se consideran independientes unas de otras. El proceso de razonamiento en este nivel se lleva a cabo a través de la identificación de los componentes y atributos de las figuras, con la finalidad de caracterizar a los integrantes de una clase o familia de objetos. Por ejemplo, si se menciona a los estudiantes que un cuadrilátero dibujado tiene cuatro ángulos rectos, serán capaces de identificarlo como un rectángulo, aunque el dibujo se haya hecho sin mucha precisión.
Los estudiantes que se encuentran en este nivel son capaces de descubrir empíricamente propiedades de una clase de figuras, aunque sin establecer relaciones entre ellas; es decir, las considera de forma independiente. Por ejemplo, si a los estudiantes se les muestra la Figura 2 y se les pide que coloreen los ángulos que tienen la misma medida, podrán determinar que los ángulos opuestos de los paralelogramos son iguales (Crowley, 1987), pero sin ser capaces de justificar por qué esto es así. Lo anterior significa que los estudiantes no entienden la estructura lógica de las definiciones como conjuntos de propiedades necesarias y suficientes que caracterizan a un objeto geométrico. Cuando se les pide que expresen la definición de un objeto geométrico, generalmente enlistarán propiedades del objeto sin detectar la redundancia de algunas propiedades (un cuadrado es un polígono que tiene cuatro lados iguales, dos pares de lados paralelos, sus ángulos miden 90°, sus diagonales son iguales y perpendiculares); o elaborarán una lista en la que no se incluyen algunas propiedades necesarias que se consideran implícitamente (un cuadrado es un polígono que tiene cuatro lados iguales) (Gutiérrez y Jaime, 1998).
En este nivel los estudiantes únicamente pueden llevar a cabo clasificaciones exclusivas, por ejemplo, son capaces de determinar que los rectángulos no son cuadrados, pero no necesariamente identificarán a un cuadrado como un rectángulo o como un rombo, o a un rectángulo como un paralelogramo. Es decir, aún no son capaces de establecer que una misma figura puede pertenecer a varias clases generales o familias, y poseer varios nombres.
Nivel 3: Ordenación, clasificación o abstracción. Los estudiantes interrelacionan lógicamente propiedades de los conceptos, construyendo o siguiendo argumentos informales. Los estudiantes que se encuentran en este nivel son capaces de formular definiciones abstractas, es decir, señalar las condiciones necesarias y suficientes que debe satisfacer una clase de figuras geométricas, además de reconocer cómo unas propiedades de los objetos geométricos se derivan de otras, estableciendo relaciones entre propiedades y las consecuencias de esas relaciones. Por ejemplo, en este nivel los estudiantes son capaces de determinar que un triángulo que tiene tres lados iguales, también tiene tres ángulos iguales. Los estudiantes son capaces de formular justificaciones informales de resultados matemáticos, por ejemplo, al justificar por qué un cuadrado es un rectángulo o por qué la suma de los ángulos en cualquier triángulo es igual a 180°. En este nivel el significado intrínseco de la deducción, es decir, el papel de los axiomas, definiciones y teoremas no se comprende completamente (van Hiele, 1999).
Nivel 4: Deducción Formal. Los estudiantes prueban teoremas deductivamente y establecen relaciones entre teoremas. Entienden la necesidad de justificar deductivamente resultados matemáticos o proposiciones, con base en un sistema axiomático. El estudiante es capaz de demostrar un resultado de diferentes formas.
Nivel 5: Rigor. Los estudiantes establecen teoremas en diferentes sistemas axiomáticos y analizan o comparan esos sistemas. Se conoce la existencia de diferentes sistemas axiomáticos y se pueden analizar y comparar. El estudiante es capaz de realizar deducciones abstractas. El razonamiento geométrico en este nivel es bastante abstracto y no necesariamente involucra el uso de modelos pictóricos o concretos. En este nivel los postulados o axiomas son objeto de análisis y escrutinio.
Los niveles de pensamiento geométrico se caracterizan por las diferencias en los objetos de pensamiento que son el centro de su atención. Por ejemplo, en el nivel 1 los objetos de pensamientos son figuras geométricas. En el nivel 2 el estudiante opera sobre ciertas clases de figuras y descubre propiedades en esas clases. En el nivel 3 las propiedades son el objeto sobre el cual los estudiantes actúan obteniendo ordenamientos lógicos de las mismas. En el nivel 4 las relaciones ordenadas son el objeto que los estudiantes operan y en el nivel 4 los objetos de pensamiento son los fundamentos de esas relaciones de ordenamiento (Fuys, Geddes y Tischler, 1988).
Los niveles cuentan con cinco propiedades, las cuales se enuncian a continuación:
Propiedad 1. (Secuencia fija) Un estudiante no puede estar en el nivel de van Hiele n, si no ha pasado por el nivel n-1.
Propiedad 2. (Adyacencia) En cada nivel de pensamiento, lo que era intrínseco en el nivel anterior se vuelve extrínseco en el nivel actual.
Propiedad 3. (Distinción) Cada nivel tiene sus propios símbolos lingüísticos y su propia red de relaciones que conectan esos símbolos.
Propiedad 4. (Separación) Dos personas que razonan en diferentes niveles pueden tener dificultades para entenderse mutuamente.
Propiedad 5. (Logro) El proceso de aprendizaje que lleva a un entendimiento completo, es decir al siguiente nivel más alto se compone de cinco fases (Usiskin, 1982).
El objetivo de estas fases es proporcionar elementos que permitan al profesor diseñar actividades y organizar escenarios de instrucción que permitan a los estudiantes avanzar en los sucesivos niveles de pensamiento geométrico.
Fase 1: Información o indagación. El estudiante se familiariza con el dominio de trabajo. En esta fase el profesor y los estudiantes se involucran en una discusión acerca de los objetos de interés de cada nivel. Se realizan observaciones, se generan preguntas y se introduce vocabulario específico. Algunas de las preguntas que puede formular el profesor son ¿qué es un paralelogramo? ¿Qué es un cuadrado? ¿Qué es un rectángulo? ¿Qué tienen en común las figuras anteriores? ¿En qué son diferentes? ¿Es posible que un rectángulo sea un paralelogramo o que un paralelogramo sea un rectángulo? Los objetivos de las actividades anteriores es que el profesor determine cuáles son los conocimientos que el estudiante posee y que el estudiante perciba cuál es el rumbo que tomará el proceso de instrucción (Crowley, 1987).
Fase 2: Orientación guiada. Los estudiantes exploran un tema de estudio a través de actividades propuestas por el profesor. Mediante el desarrollo de estas actividades, los estudiantes llevarán a cabo procesos del pensamiento matemático relevantes para cada nivel. La actividad del profesor consiste en formular preguntas que tengan una respuesta concreta, pero de forma que la búsqueda de la respuesta favorezca la reflexión y la comunicación de ideas. Por ejemplo, el profesor puede solicitar a los estudiantes que construyan, en una cuadrícula o un geoplano, un rombo con diagonales iguales, un rombo con diagonales diferentes; que construya rombos con uno, dos, tres y cuatro ángulos rectos; o que construya un cuadrado de área 2.
Fase 3: Explicitación o explicación. El estudiante es consciente de las relaciones que existen entre las propiedades de los objetos geométricos, trata de expresarlas verbalmente o por escrito y aprende el lenguaje técnico que acompaña a la materia. A partir de sus experiencias previas, durante el desarrollo de las actividades propuestas por el profesor, los estudiantes expresan e intercambian sus puntos de vista con el objetivo de construir relaciones.
Fase 4: Orientación libre. El estudiante aprende mediante la ejecución de tareas que tienen diferentes soluciones o son de respuesta abierta. A través de la actividad matemática que desarrollan los estudiantes, se promueve la construcción de redes complejas de relaciones entre conceptos y procesos matemáticos relevantes para cada nivel. Las tareas permiten al estudiante explorar, formular conjeturas y justificar relaciones, en esta fase las conexiones y relaciones entre los objetos matemáticos empiezan a ser explícitas para los estudiantes. Un ejemplo de las tareas que se pueden utilizar durante esta fase es: encontrar una fórmula para calcular el área de un polígono construido en el geoplano, con base en el número de puntos en la frontera y en el interior del polígono, o encontrar el área de un polígono sin puntos de la malla en su interior si se conoce el número de puntos en la frontera del polígono (Figura 3).
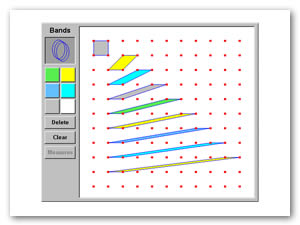
Figura 3. ¿Cuál es el área de las figuras con tres y cuatro puntos en la frontera, y sin puntos en el interior?
Fase 5: Integración. El estudiante resume todo lo que ha aprendido acerca del tema, entonces reflexiona sobre sus propias acciones y obtiene una visión general de la nueva red de relaciones que se construyó durante el trabajo con las actividades de instrucción. El papel de profesor en esta fase consiste en explicitar relaciones o procesos que los estudiantes aprendieron. Teóricamente, al final de la quinta fase, los estudiantes habrán logrado un nuevo nivel de pensamiento y están listos para iniciar el trabajo que los conduzca a alcanzar un nuevo nivel.
Un hecho importante es que el tránsito entre niveles es un proceso continuo que no se lleva a cabo de forma inmediata, más bien requiere de tiempo y experiencias de instrucción apropiadas; esto significa que el tipo de tareas que los estudiantes abordan en el salón de clase determinan los procesos cognitivos y las características del aprendizaje que los estudiantes logran construir. Si un profesor trata de que un estudiante aprenda los procesos y habilidades relevantes de un nivel, a través de cierto conjunto de actividades, sin que el estudiante haya dominado los procesos de los niveles previos, lo más probable es que el estudiante no pueda abordar las actividades o que las mismas no le permitan llevar a cabo procesos cognitivos de alto nivel (propiedad 4), con lo cual, en el mejor de los casos, se conseguirá únicamente un aprendizaje memorístico.
Cabe resaltar que el nivel de razonamiento es local; es decir, se posee un nivel de razonamiento por cada concepto o idea geométrica. Un estudiante que se encuentra en el nivel 3 al razonar sobre polígonos, puede encontrarse en el primer nivel de razonamiento al estudiar isometrías (Zambrano, 2006). Por otra parte, el logro de los sucesivos niveles no es una cuestión puramente biológica, sino que es esencialmente un producto de las características del proceso de instrucción.
Una actividad central del profesor de matemáticas consiste en determinar con precisión el nivel de razonamiento que poseen los estudiantes, para cada concepto o contenido específico, con la finalidad de establecer cuáles son las actividades y escenarios de instrucción apropiados para lograr una consolidación de los procesos mentales característicos de un nivel o el tránsito hacia un mayor nivel de entendimiento.
Burger, W. F. & Shaughnessy, J. M. (1986). Characterizing the van Hiele Levels of Development in Geometry. Journal for Research in Mathematics Education, 17(1), 31-48.
Crowley, M.L. (1987). The van Hiele model of the development of geometric thought. En M. M. Lindquist (Ed.), Learning and teaching geometry, K-12 (pp. 1-16). Reston, VA: National Council of Teachers of Mathematics.
Fuys, D., Geddes, D. &Tischler, R. (1988).The van Hiele model of thinking in geometry among adolescents. Journal for Research in Mathematics Education Monograph Number 3. Reston, VA: National Council of Teachers of Mathematics.
Guillén-Soler, G. (2004). El modelo de van Hiele aplicado a la geometría de los sólidos: describir, clasificar, definir y demostrar como componentes de la actividad matemática. Educación Matemática, 16(3), 103-125.
Gutiérrez, A. & Jaime, A. (1988). On the assessment of the van Hiele levels of reasoning. Focus on Learning Problems in Mathematics, 20(2, 3), 27-46.
Peg, J. (2014). The van Hiele theory. En S. Lerman (Ed.), Encyclopedia of Mathematics Education (pp. 613-615). Dordrecht: Springer.
Usiskin, Z. (1982). Van Hiele levels and achievement in secondary school geometry (Final Report of the Cognitive Development and Achievement in Secondary School Geometry Project). Chicago, IL: University of Chicago, Department of Education.
van Hiele, P. M. (1999). Developing geometric thinking through activities that begin with play. Teaching Children Mathematics, 6, 310-316.
Zambrano, M. A. (2006). El razonamiento geométrico y la teoría de van Hiele. Kaleidoscopio, 3(5), 28-33.
[a] Profesor Investigador del Área Académica de Matemáticas y Física de la UAEH. Es Licenciado en Física y Matemáticas por la Escuela Superior de Física y Matemáticas del IPN y Doctor en Ciencias por la Universidad de Arizona. Sus líneas de investigación son Teoría de números y resolución de problemas en el aprendizaje de las matemáticas
[b] Profesor Investigador del Área Académica de Matemáticas y Física de la UAEH. Es Actuario por la Facultad de Ciencias de la UNAM y doctor en ciencias con la especialidad en Matemática Educativa por el Departamento de Matemática Educativa del CINVESTAV-IPN. Su línea de investigación es resolución de problemas y uso de las tecnologías digitales en el desarrollo de entendimiento matemático.