Este documento analiza el efecto de la inequitativa distribución funcional del ingreso en el crecimiento económico mexicano de 1980 a 2013. En la teoría económica no existe un consenso sobre el efecto que tiene la distribución del ingreso sobre el crecimiento económico, Kaldor (1956) propone que la concentración del ingreso a favor de los capitalistas fomenta el crecimiento, en contraste, Keynes (1936) y Kalecki (1982) argumentan que una equitativa distribución del ingreso, entre capitalistas y asalariados, genera crecimiento. El aporte de este ensayo es examinar el impacto de la desigualdad en la distribución del ingreso en el crecimiento económico en México a través de un modelo econométrico. Los resultados obtenidos muestran que la concentración del ingreso en la clase capitalista afecta negativamente al crecimiento.
Palabras clave:Distribución del ingreso y crecimiento económico JEL D33 O40.
This paper analyzes the effect of functional inequitable income distribution in the Mexican economic growth in 1980-2013. In economic theory there is no consensus on the effect of income distribution on economic growth, Kaldor (1956) proposes that the concentration of income in favor of capitalists promotes growth, in contrast, Keynes (1936) and Kalecki (1982) argued that equitable income distribution between capitalists and workers generates growth. The contribution of this paper is to examine the impact of inequality in income distribution on economic growth in Mexico through an econometric model. The results show that the concentration of income in the capitalist class has negative effects on growth.
Keywords: Income Distribution and Economic Growth JEL D33 O40.
La distribución funcional del ingreso representa el modo característico y directo de asignación de la renta nacional entre los componentes principales, trabajadores y capitalistas, de un sistema económico.
La relación entre la desigualdad en la distribución funcional del ingreso y el crecimiento económico ha despertado varias opiniones a lo largo del tiempo, están las que sostiene que la desigualdad en la distribución afecta negativamente al crecimiento y otras que demuestran que dicha desigualdad lo favorece. Desde los autores clásicos como David Ricardo y Karl Marx, ya se planteaba la disputa entre los capitalistas y los asalariados por el ingreso nacional. La teoría de Kaldor (1956) propone que la concentración del ingreso incrementa las posibilidades del crecimiento, debido a que los capitalistas tienen más propensión a ahorrar y con ello a invertir, que los asalariados, y así incrementar el crecimiento.
Por el contrario, la teoría que sostiene que el crecimiento necesita de una distribución igualitaria se conoce como “de compatibilidad unidireccional”. Fue en el siglo XX que esta teoría tuvo una aportación destacada a cargo de Keynes (1936). Aseguraba que si hay una mejor distribución del ingreso de las capas con mayor participación en el ingreso hacia los sectores con menor participación, traerá consigo un mayor consumo, lo cual incentivará la demanda efectiva y con ello la producción y el empleo.
Kalecki (1982) sostiene que una mejor distribución puede traer consigo crecimiento. De acuerdo con este autor un incremento en el salario provoca que crezca el consumo de los trabajadores, aumentando así la demanda efectiva, la mayor demanda efectiva incentiva el crecimiento de la inversión y con ello el de la economía en su conjunto.
México ha presentado una desaceleración importante en su crecimiento económico, en promedio anual, según datos del Banco Mundial, ha crecido sólo un 2.5 por ciento en el periodo 2003 a 2012.
Además de una alta desigualdad en la distribución funcional del ingreso causada por la disminución en la participación de los asalariados en el ingreso y un aumento de la participación por parte de los capitalistas.
En la literatura empírica usualmente se estudia cómo afecta la distribución del ingreso al crecimiento económico a partir del coeficiente de Gini, es decir, bajo una distribución personal.
En contraste, en la presente investigación se ocupan las variables: excedente bruto de operación y remuneración de asalariados, para analizar el impacto que ha tenido la desigualdad en la distribución funcional del ingreso en el crecimiento económico de México, con la finalidad de determinar cuánto ha contribuido esta inequidad en la desaceleración del crecimiento para el periodo de 1980 a 2013, mediante la aplicación de un modelo econométrico.
Este documento se divide en tres apartados, en el primero se presenta una breve descripción de la literatura empírica sobre la distribución del ingreso y su impacto en el crecimiento económico. El segundo apartado refiere la metodología a utilizar, así como el análisis de los resultados. Finalmente se presentan las conclusiones.
Estudios empíricos
Existen diversos estudios empíricos sobre la distribución funcional y su relación con el crecimiento de las economías. Lindenboim, Kennedy y Graña (2005) analizan la participación de los asalariados en el Producto Bruto Interno (PIB), para lo cual calculan un cociente de masa salarial[1] , encuentran que en el periodo de 1950 a 1973 la participación de los asalariados era del 44 por ciento, sin embargo, para el año 2001 se redujo al 32 por ciento. Gaviria (2005), mediante un ejercicio econométrico, cuya variable dependiente es la tasa real de crecimiento del PIB per cápita y la independiente es el coeficiente de Gini, argumenta que la desigualdad ha limitado el crecimiento económico en las regiones colombianas. Piñón (1994) analiza los factores que determinan la participación de los salarios en el ingreso y verifica la extensión de la teoría distributiva de Kalecki, los resultados muestran que una proporción (0.11) de la variación en la participación de los salarios en el ingreso nacional es explicada por la variación de los precios internacionales contra los salarios reales, para México en el periodo 1970-1992. Por último, Ríos (2003) identifica el efecto final de la desigualdad del ingreso sobre el crecimiento económico, mediante un ejercicio con datos de panel en las entidades federativas de México durante el periodo de 1984 a 1999, encuentra una relación negativa y significativa del coeficiente de Gini con el crecimiento del PIB per cápita real, esto sugiere que en promedio los estados con un nivel más alto de desigualdad tienden a crecer a una tasa menor que los estados con un ingreso más equitativo.
Metodología
Variables utilizadas
a) Producto Interno Bruto y Tasa de Crecimiento. En primer lugar se ocupan el PIB anual a precios constantes (base 2008) para México y su tasa de crecimiento.
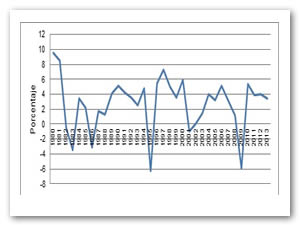
La tasa de crecimiento (TC) exhibe periodos de retracción y otros de expansión. Llegando a un máximo de 9.4 por ciento al inicio del periodo y un mínimo de -6.2 por ciento en 1995.
Desde 1980 la tasa de crecimiento no ha vuelto a estar cerca del máximo, y el promedio de crecimiento en estos años ha sido de apenas 2.7 por ciento (gráfica 1).
Gráfica 1. Tasa de Crecimiento del PIB a precios constantes de 2008, 1980-2013.
Fuente: Elaboración propia con datos del Banco Mundial.
b) Excedente bruto de operación Se considera al excedente bruto de operación como variable proxy para calcular la participación de los capitalistas en el ingreso total. Se convierte el valor nominal a valor constante, con la misma base que el PIB, para evitar los efectos de la inflación (ecuación 1).
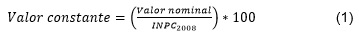
La serie muestra una tendencia a la alza a lo largo del periodo, con ligeras caídas en años de crisis en la economía mexicana, empero, es a partir del año 2000 que el excedente muestra un mayor crecimiento (gráfica 2).
Gráfica 2: Excedente Bruto de Operación a precios constantes de 2008, 1980-2013.
Fuente:Elaboración propia con datos del INEGI, Sistema de cuentas nacionales.
c) Remuneración de asalariados Según el Banco de México, la remuneración de asalariados incluye los pagos que los empleadores efectúan a los fondos de la seguridad social, así como a las empresas de seguros o a otras unidades institucionales encargadas de la administración y gestión de sistemas de seguridad social. Esta variable será útil para representar la participación de los trabajadores en el producto. La serie tiene una tendencia ascendente (gráfica 3), no obstante, mientras que en 2013 el excedente fue de 9,102,322.40 millones de pesos a precios de 2008, la remuneración de asalariados fue 3,679,524.13 millones de pesos.
Gráfica 3: Remuneración de Asalariados a precios constantes de 2008, 1980-2013
Fuente:Elaboración propia con datos del INEGI, Sistema de cuentas nacionales.
El modelo econométrico que se estima es:
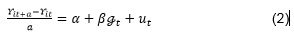
Donde:
Υ_(t ): Tasa de crecimiento del PIB nacional a precios constantes
a : Periodo de 1980 a 2013
α : Intercepto
g_t: Tasa de crecimiento de la desigualdad en la distribución del ingreso entre los asalariados y los capitalistas durante los treinta años
u_t : Término de error
El objetivo es estimar la elasticidad de la desigualdad en la distribución del ingreso con relación al crecimiento del PIB, para verificar el grado de sensibilidad, en términos porcentuales, de la tasa de crecimiento del PIB nacional ante cambios en la distribución funcional.
Participación de las clases
Para el cálculo de la distribución funcional del ingreso se utiliza como indicador la participación de los asalariados en el ingreso nacional disponible (PAI), de la siguiente forma:
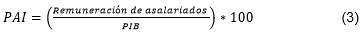
Mientras que la participación de los capitalistas en el ingreso nacional (PCI):
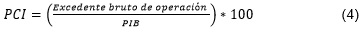
Estimaciones
Durante el periodo de estudio la participación de los capitalistas (PC) ha tenido un máximo de 69.2 por ciento en el año 2012, mientras que la participación de los
asalariados (PA) alcanzó un máximo de 37.4 por ciento en 1981 (gráfica 4). Por su parte los impuestos a la producción y a las importaciones se mantuvieron constantes hasta la década de los 2000, posterior a este periodo, la tendencia fue decreciente.
Gráfica 4: Participación de Capitalistas, Asalariados e Impuestos en el Ingreso Nacional, 1980-2013 Fuente: Elaboración propia con datos del INEGI, Sistema de cuentas nacionales.
A partir del año 2000 la desigualdad entre PC y PA, ha tenido un comportamiento creciente (gráfica 5).
Gráfica 5: Desigualdad en la Distribución Funcional del Ingreso, 1980-2013
Fuente:Elaboración propia con datos del INEGI, Sistema de cuentas nacionales.
Una vez obtenidas las series es conveniente analizar si son o no estacionarias, para tal efecto se aplicaron tres pruebas, Dickey Fuller Aumentada (ADF) (Dickey y Fuller, 1979), Kwiatkowski, Phillips, Smichdt y Shin (KPSS) (Kwiatkowski, Phillips, Schmidt y Schin, 1992), y Phillips Perron (PP) (Phillips y Perron, 1988). En relación a la variable desigualdad (DES), no se rechaza la hipótesis de que la serie presenta raíz unitaria en dos de las tres pruebas efectuadas, a un nivel de confianza del 95 por ciento y se considera no estacionaria.
En la variable TC, se rechaza la hipótesis nula en todas las pruebas, al mismo nivel de confianza, por lo que la serie es estacionaria (tabla 1). Cuando las series no son estacionarias lo recomendable es llevar a cabo el método de cointegración de Johansen (1988) para estimar las elasticidades; no obstante, en este caso no es posible realizarlo, por lo que se calculan las tasas de crecimiento de ambas series y se realiza un ejercicio econométrico con el método de cuadrados mínimos ordinarios.
Tabla 1: Pruebas de raíz unitaria
Fuente:Elaboración propia.
La ecuación a estimar es:
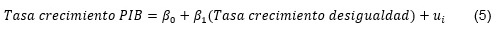
El modelo estimado es:
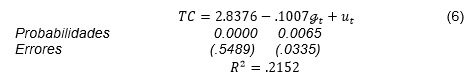
Para probar la existencia o no de estabilidad se aplicaron las pruebas Cusum y Cusum2. El primero hace una prueba de comportamiento de los residuos que generan las estimaciones recursivas[2] , y el segundo consiste en emplear los cuadrados de los residuos recursivos para comprobar desviaciones no aleatorias desde su línea de valor medio.
Gráfica 6: Prueba Cusum.
Fuente:Eviews.
Gráfica 7: Prueba Cusum Cuadrado.
Fuente:Eviews.
Para aceptar la estabilidad del modelo, la línea de valor medio debe permanecer dentro de las líneas críticas (segmentadas). En este caso es posible aceptar la hipótesis de estabilidad en los parámetros del modelo porque se encuentra dentro a lo largo del periodo.
Para la detección de heteroscedasticidad se realizó la prueba de White, la cual rechaza la hipótesis de la existencia de heteroscedasticidad y para la autocorrelación se analiza el estadístico Durbin-Watson (2.01), que demuestra la no existencia de autocorrelación. Por último, el parámetro de la tasa de crecimiento de la desigualdad es estadísticamente significativo, por lo que las fluctuaciones de esta variable explican los cambios en la variable dependiente.
Debido a que únicamente es necesario identificar el parámetro β, es decir el valor de la elasticidad, se realiza una estimación bivariada, por lo que no es imperiosa la inclusión de otras variables. Cabe precisar que el interés de la investigación es analizar el modelo a través de tasas de crecimiento de la desigualdad y del crecimiento del PIB, por ello es que no se construye un modelo con valores rezagados de las variables.
La estimación arroja una elasticidad de -0.1007 por ciento, es decir, ante un cambio en un punto porcentual en la tasa de crecimiento de la desigualdad, la tasa de crecimiento del PIB disminuirá en 0.10 por ciento aproximadamente. En conclusión, la desigualdad en la distribución funcional del ingreso ha tenido un impacto negativo en el crecimiento económico de México de 1980 a 2013.
Por lo anterior, se convierte en prioridad reducir la desigualdad para que se pueda obtener el círculo de beneficios al que se refieren tanto la teoría keynesiana como la kaleckiana, lo cual conduciría a una igualitaria distribución entre los dos agentes económicos.
La distribución asimétrica del ingreso es uno de los principales problemas que agobia a la sociedad mexicana, no sólo porque es moralmente cuestionable que la riqueza sea concentrada en una pocas manos, mientras una gran mayoría sufre carencias y pobreza extrema, sino porque además esto tiene implicaciones importantes sobre el crecimiento económico y, por tanto, sobre el bienestar material de las futuras generaciones.
En este trabajo se analiza cómo la distribución del ingreso entre trabajadores y capitalistas condiciona el crecimiento económico en México. Se muestra que si la tasa de crecimiento de la concentración del ingreso aumenta en uno por ciento, entonces la tasa de crecimiento de la economía se reducirá en 0.10 porciento.
Este resultado es contradictorio con lo postulado por Kaldor (1956), pero es coincidente con lo señalado por Keynes (1936) y Kalecki (1982). Por lo que, se podrían utilizar estas teorías para proponer recomendaciones de política económica encaminadas a reducir la inequidad en la distribución del ingreso, con la finalidad de mejorar tanto el nivel de vida de las generaciones presentes como fomentar el crecimiento económico.
Araya (1996). Pruebas de estabilidad denominadas Cusum y Cusum cuadrado. Costa Rica: Banco Central de Costa Rica.
Dickey y Fuller (1979). Distribution of the Estimators for Autoregressive Time Series With a Unit Root, Journal of the American Statistical Association, Vol. 74, No. 366, June, pp. 427-431.
Gavira (2005). Distribución del ingreso y crecimiento económico. Economía y Desarrollo , Bogotá.
Johansen (1988). Statistical Analysis of Cointegration Vectors. Journal of Economic Dynamic and Control, vol. 12, pp. 231-254.
Kaldor (1956). Alternative Theories of Distribution, Review of Economic Studies, Vol. 23, No. 2, pp. 83-100.
Kalecki (1982). Ensayos escogidos sobre dinámica de la economía capitalista, Fondo de Cultura Económica, México.
Keynes (1936). The General Theory of Employment, Interest, and Money. New York: Harcourt, Brace & World.
Kwiatkowski, Phillips, Schmidt, y Schin (1992). Testing the null hypothesis of Stationarity against the alternative of a unit root. How sure are we that economic time series have a unit root?. Journal of Econometrics, 54, pp. 159-178, North-Holland.
Lindenboim, Kennedy y Graña (2005). Distribución Funcional del ingreso en Argentina. Ayer y Hoy. Documentos de trabajo 4, Buenos Aires, CEPED, FCE-UBA.
Loaiza, O. (2011). La demanda agregada y la distribución del ingreso: Un estudio a partir de los modelos de crecimiento kaleckianos. Colombia: MPRA Paper.
Mata, H. (2005). Nociones Elementales de Cointegración Enfoque de Soren Johansen. Perú: Universidad de los Andes.
Phillips, P. and Perron P. (1988). Testing for a Unit Root in Time Series Regression. Biometrika, 75, pp. 335-346.
Piñon, F. (2003). Distribución Funcional en México, Un enfoque Neo-Kaleckiano. D.F.: UAM
Rios, S. (2003). Efectos de la desigualdad del ingreso sobre el crecimiento económico: un análisis por entidad federativa para México. Ensayos-Volumen XXII, 89-122.
Villavicencio, J. (2011). Introducción a series de tiempo. México.
Banxico (2013). Glosario de términos. Recuperado el 17 de Abril de 2014, de http://www.banxico.org.mx/divulgacion/glosario/glosario.html
Banxico. (2014). Glosario de terminos . Recuperado el 21 de FEBRERO de 2014, de Glosario de terminos:
http://www.banxico.org.mx/divulgacion/glosario/glosario.html
Economia, E. d. (Septiembre de 2008). La gran enciclopedia de economia. Recuperado el 17 de Abril de 2014, de La gran enciclopedia de economia:
http://www.economia48.com/spa/d/ganancia/ganancia.html
INEGI. (s.f.). INEGI. Recuperado el 12 de Abril de 2014, de INEGI: http://www.inegi.org.mx/
[0] Este documento es resultado del proyecto final de investigación para obtener el grado de Licenciada en Economía de la estudiante Estefanía Aguilar Castro.
[1] Masa salarial es el producto entre el salario medio y total de asalariados (Gavira, 2005:25).
[2] Por estimaciones recursivas se entienden aquellas en que la ecuación se estima repetidamente (Araya, 1996:6).
[b] Estudiante del noveno semestre de la Licenciatura en economía de la Universidad Autónoma del Estado de Hidalgo.
[a] Profesora Investigadora de Tiempo Completo del Instituto de Ciencias Económico Administrativas del Área Académica de Economía de la UAEH.
[a] Profesor Investigador de Tiempo Completo del Instituto de Ciencias Económico Administrativas del Área Académica de Economía de la UAEH.