El estudio de la ecuación cuadrática en el contexto geométrico pretende la conexión de conceptos fundamentales en torno a la ecuación cuadrática, logrando así la interpretación geométrica de las raíces de una ecuación cuadrática.
Dicha interpretación se llevará acabo mediante la construcción de una familia de rectángulos, que permitan examinar el comportamiento de la diferencia o suma de áreas, y de esta manera generar la gráfica de una función cuadrática interpretando geométricamente las raíces asociadas a su ecuación cuadrática.
Palabras clave: Ecuación cuadrática, interpretación geométrica, raíces.
The Study of the quadratic equation in the geometric context aims the connection fundamental concepts about the quadratic equation, achieving the geometric interpretation of the Roots of a quadratic equation.
Such interpretation will be helded by building a rectangle family, which allows to examinate the behavior on the difference or the adding of the areas, and in this way generate the graphic of a quadratic function interpreting geometrically the associated roots to a quadratic equation.
Keywords: Quadratic equation, geometric interpretation, roots
Iniciaremos con la construcción de una familia de cuadrados y rectángulos, la cual se realizará con el empleo de un software dinámico (Cabri Geometry), dicho software es fácil de utilizar y además cuantifica de manera sencilla distancias, perímetros, áreas, determina ecuaciones, y en general permite analizar el comportamiento de la diferencia de áreas, así el alumno podrá conjeturar, analizar y conectar conceptos referentes a la ecuación cuadrática.
Esta representación dinámica nos permite interpretar a la función cuadrática como la diferencia de áreas de un rectángulo con dos cuadrados, en donde la base del rectángulo y los lados de un cuadrado son variables, mientras la altura del rectángulo permanece fija así como el área y los lados del segundo cuadrado.
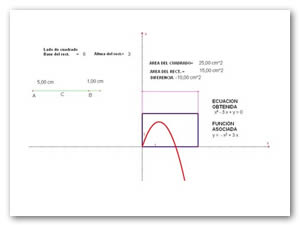
Si consideramos que la ecuación cuadrática -x2 + 3x + 2= 0 tiene como función asociada a y = - x2 + 3x + 2, sabemos que la gráfica de dicha función corresponde a una parábola, sin embargo podemos obtener esta parábola mediante la resta o suma del área de dos cuadrados con un rectángulo.
Por ejemplo:
Para la función y = -x2 + 3x + 2, podemos considerar que x2 representa el área de un cuadrado (variable) de lado x, 3x representa el área de un rectángulo (variable) de base x y altura igual a 3, y el término 2 representa el área de un cuadrado (fijo) de lado √2. Entonces si al área del rectángulo y del cuadrado fijo le restamos el área del cuadrado variable, la diferencia nos permite obtener una función cuadrática.
Utilizando el software cabri geometry realizaremos la construcción de las figuras geométricas que nos permitirán representar los términos de la ecuación cuadrática - x2 + 3x= 0 y mediante la diferencia de áreas obtener la gráfica de la función cuadrática y = -x2 + 3x Sabemos que x2 representa el área del cuadrado y 3x representa el área del rectángulo de base x y altura 3, entonces para obtener la gráfica de la función y = - x2 + 3x debemos restar al área del rectángulo el área del cuadrado. Como se muestra a en la figura 1.
Figura 1
En la figura 1 podemos relacionar a x2 con el área del cuadrado, mientras que 3x representa el área del rectángulo, como se aprecia en la gráfica y dicha diferencia de áreas permite obtener la gráfica de una función cuadrática.
A través de la construcción dinámica de la función cuadrática podemos analizar diversos aspectos concernientes a la ecuación cuadrática. Por ejemplo, si tratamos de aproximar la diferencia de áreas a cero, podemos observar que ocurre con el área del rectángulo y del cuadrado, como se observa en la figura 2.
Figura 2
Figura 3
En este caso se pretende aproximar la diferencia de áreas a cero, y como podemos observar en la figura 3 el área del cuadrado se aproxima al área del rectángulo, por lo tanto las figuras geométricas también se van aproximando.
Figura 4
En la figura 4 podemos observar que la diferencia de áreas del cuadrado y del rectángulo se aproxima a cero, por lo tanto el cuadrado y el rectángulo se aproximan cada vez más.
Figura 5
En la figura 5 podemos observar que cuando la diferencia de áreas es cero, ambas figuras geométricas coinciden, por lo que el cuadrado y el rectángulo tienen la misma área. Cuando ambas áreas son iguales, dos vértices del cuadrado intersecan al eje x en dos puntos como se aprecia en la gráfica de la figura 5.
En la tabla 1 podemos observar como al hacer variar a x, el área del cuadrado y el rectángulo también varían, generando así con la diferencia de ambas áreas los pares ordenados que permiten graficar la función y = - x2 + 3x mostrada en la figura 6.
Tabla 1
Es importante considerar que cuando la diferencia de áreas es cero, tanto el rectángulo como el cuadrado alcanzan la misma área, y además al superponerse las figuras geométricas por tener la misma área, dos vértices del cuadrado coinciden con las raíces de la función cuadrática.
Otro aspecto importante es considerar el parámetro c de la ecuación cuadrática, entonces si c representa una constante podemos observar el comportamiento de la gráfica de la función cuadrática cuando asignamos un valor para c. Por ejemplo, para la ecuación cuadrática -x2 + 3x = 0 su función asociada es y = - x2 + 3x, y sabemos que la gráfica de dicha función corresponde a una parábola, la cual se obtuvo mediante la diferencia de áreas de un rectángulo con un cuadrado, entonces la ecuación cuadrática ax2 + bx = 0 puede representarse en términos de áreas y de esta manera obtener la gráfica de la función cuadrática asociada es f(x) = ax2 + bx.
La gráfica de la función y = - x2 + 3x se muestra en la figura 6:
Figura 6
De acuerdo a los anterior hemos representado los términos - x2 + 3x = 0 de una ecuación cuadrática mediante la diferencia de áreas, donde x2 es un cuadrado de lado x mientras que 3x es un rectángulo de base x y altura 3.
Sin embargo una ecuación cuadrática de la forma ax2 + bx + c = 0, puede ser interpretada a través del manejo de áreas, de esta manera el término c también lo podemos representar mediante un cuadrado de área fija, es decir un cuadrado de área fija igual a = c y lado = √c.
Por ejemplo:
La ecuación cuadrática -x2 + 6x - 5 = 0, en términos de áreas de acuerdo a lo planteado anteriormente; se interpreta gráficamente como se ilustra en la figura 7 observemos el comportamiento gráfico de la función cuadrática asociada en la figura 7 si en este caso c = 5.
Gráfica de la función asociada y =-x2 + 6x – 5.
Figura 7
En la gráfica de la figura 7 podemos observar que cada uno de los términos de la expresión x2 + bx + c = 0 pueden representarse a través del área de figuras geométricas, es decir x2 corresponde al área de un cuadrado de lado x, bx corresponde a un rectángulo de base x y altura fija b, de esta manera el término c corresponde al área fija de un cuadrado de lado √c y en la gráfica lo identificamos como el cuadrado con relleno, de manera que a través de la diferencia de áreas nos permite obtener la gráfica de su función cuadrática asociada y = x2 + bx + c
Entonces cada uno de los términos de la ecuación cuadrática -x2 + 6x – 5= 0 están representados a través del área de figuras geométricas, en donde la diferencia de áreas nos permite obtener la gráfica de su función cuadrática asociada y = -x2 + 6x -5, como se observa en la figura 7.
Figura 8
Figura 9
Observe en la gráfica de la figura 8 y 9 que el término c esta representado a través de un cuadrado de área fija = 5cm2 y lado √c≈ 2.23cm2.
De esta manera cada uno de los términos de la ecuación cuadrática -x2 + 6x – 5= 0 están representados a través del área de figuras geométricas y la diferencia de dichas áreas nos permite obtener la gráfica de la función cuadrática asociada y = x2 + 6x – 5.
De acuerdo al análisis anterior podemos determinar que una ecuación cuadrática ax2 + bx + c = 0 asociada a una función cuadrática y = ax2 + bx + c puede ser representada en el contexto geométrico como:
Algunos aspectos que pueden comenzar a explotarse con esta construcción dinámica son los siguientes:
Hitt, F. (2002). Funciones en Contexto. México. Pearson Educación.
Steen, A. (2001). La enseñanza agradable de las matemáticas. México. Limusa S. A. de C.V.
Steward, J. (2001). Cálculo, conceptos y contextos. Thomson.
[a] Profesor de la Universidad Autónoma del Estado de Hidalgo.