Solución de un Sistema de Ecuaciones Simultáneas de Dos incógnitas por los métodos: Sustitución, Igualación, Reducción y Gráfico.

Pedro de J. Soto-Pedraza^[a]

Resumen

Un sistema de ecuaciones simultáneas con dos incógnitas es un conjunto de dos ecuaciones donde cada una de esas dos involucra dos parámetros desconocidos o incógnitas, donde el valor que se le asigne a cada incógnita en una ecuación, es el mismo que se le deberá asignar en la otra ecuación.
Para resolver un sistema de ecuaciones simultáneas con dos incógnitas, el procedimiento a seguir es eliminar una de las dos incógnitas usando las dos ecuaciones y obtener así una sola ecuación que involucre una sola incógnita, para eliminar una de las dos incógnitas se pueden utilizar los métodos:

a) De Sustitución
b) De igualación
c) De Reducción

Para hallar una representación gráfica del resultado que satisfaga ambas ecuaciones, se utiliza el método:

d) Gráfico

Palabras clave: Ecuación, Satisfacer ambas ecuaciones, Obtener una ecuación con una sola incógnita, Encontrar la segunda incógnita a partir de conocer la primera

Abstract

A system of simultaneous equations with two unknowns is a set of two equations where each of these two involves two unknown parameters or unknowns, where the value that is assigned to each unknown in an equation is the same that should be assigned to the other equation.
To solve a system of simultaneous equations with two unknowns, the procedure to be followed is to eliminate one of the two unknowns using the two equations and thus obtain a single equation that involves a single unknown, to eliminate one of the unknowns one can use the methods:

a) Replacement
b) Equalization
c) Reduction

To find a graphical representation of the result that satisfies both equations, the method to be used is:

d) Graphic

Keywords: Equation, Satisfy both equations, Get an equation with a single unknown, Find the second unknown from knowing the first equation

Introducción

Es común que muchas veces podamos reducir un problema cotidiano en un ejercicio que tenga como objetivo hallar un parámetro desconocido en un modelo que contenga una condicionante, inclusive podemos llegarnos a encontrar con la existencia de dos o más situaciones condicionadas a cumplir una igualdad que pueden involucrar a varios parámetros desconocidos y diferentes entre sí. Al establecer nosotros un modelo matemático de estas distintas situaciones donde intervienen esos parámetros construimos un sistema de ecuaciones simultáneas, para los cuales cada uno de los parámetros desconocidos permanece constante en todas las situaciones donde se encuentren involucrados. De modo que al resolver dicho modelo matemático se habrán encontrado todos los parámetros desconocidos que cumplan correctamente con las condicionantes impuestas en cada situación.

Así pues, para llegar a la solución de este sistema, se emplean métodos algebraicos que nos permiten resolver de manera simultánea, ambas ecuaciones. Pero antes de hacer eso, ¿sabemos qué es una ecuación?

Comenzaremos entonces por definir qué es una ecuación. Le llamamos ecuación a un enunciado matemático que afirma la existencia de una igualdad entre dos cantidades, y en las cuales intervienen parámetros desconocidos a los que les llamamos incógnitas, a las que representamos con letras; donde para considerar válida o verdadera a esa afirmación, los parámetros deben de tomar valores específicos que cumplan las condicionantes establecidas.

Solución de un Sistema de Ecuaciones Simultaneas con dos incógnitas

Propiamente se trabajará en este documento con ecuaciones simultáneas de dos por dos, llamado así porque el sistema constará de dos ecuaciones, donde en cada una intervendrán dos incógnitas. Teniendo la siguiente estructura:

ax+by = c
dx+ey = f

En donde las leteas a, b, d, e; son cantidades constantes que toman un valor a partir del diseño de la situación que se plantee. Y a su vez c y f son cantidades también constantes y cuya función es establecer una igualdad condicionante con la suma de los valores anteriores. Notamos que las letras x y y permanecen en ambas ecuaciones, representando los dos parámetros desconocidos que intervienen en ambas y para los cuales se debe de hallar un valor específico que al sustituirlo en las ecuaciones cumpla perfectamente con la condición de igualdad para ambas. Es decir el valor que encontremos para x debe ser el mismo que se use en ambas ecuaciones y el valor que encontremos para y debe ser también el mismo que se use en las dos ecuaciones. Y dichos valores para x y y deben hacer cumplir la condicionante de igualdad en ambas ecuaciones.

Antes de resolver un sistema de ecuaciones simultáneas es pertinente conocer el tipo de aplicaciones que puede tener en la vida cotidiana. Analicemos el siguiente ejemplo:

Ana y Roberto trabajan en la fábrica de una empresa de electrónica y electrodomésticos, Ana está en el área de producción de celulares y Roberto en el área de producción de computadoras.

El día lunes, durante su turno, Ana fabricó 8 celulares y Roberto fabricó 5 computadoras. Por las producciones de ambos, le hicieron ganar a la empresa $61,000.00.

El día martes Ana fabricó 11 celulares y Roberto fabricó 8 computadoras. Y por las producciones de ambos le hicieron ganar a la empresa la cantidad de $89,500.00. Ana y Roberto sabían el número de productos que fabricaron cada día y también sabían la cantidad de dinero que las producciones de ambos le hicieron ganar a la empresa. Pero lo que no sabía ninguno de ellos es el precio de cada uno de los productos que fabricaban. Si se deseara conocer el precio de ambos productos, ¿Cómo se podrían determinar?

He aquí un caso cotidiano en donde podemos aplicar la solución de ecuaciones simultáneas para darle respuesta al problema planteado.

La manera de estructurar el planteamiento anterior es la siguiente:

Existen dos situaciones diferentes en donde intervienen parámetros desconocidos, dichas situaciones las entendemos como el día lunes y el día martes.

Lunes --> Ecuación 1

Martes --> Ecuación 2

 

Los dos parámetros desconocidos que están presentes  de manera constante en el día lunes y el día martes son los precios del celular y de la computadora.

x  -->  Precio del celular (permanece constante el día lunes y el día martes)

y  -->  Precio de la computadora (permanece constante el día lunes y el día martes)

 

El número de piezas fabricadas por ambos trabajadores son las cantidades constantes mediante las cuales se diseñará un modelo matemático.

Ganancia de fabricación del día lunes -->  8 (precio del celular)  + 5 (precio de la computadora)

Ganancia de fabricación del día martes -->  11 (precio del celular) + 8 (precio de la computadora)

Finalmente los precios mencionados de la ganancia por ambas producciones cada uno de los dos días, son las condicionantes de igualdad a la que tiene que cumplir el modelo matemático anterior mencionado.

Ganancia de fabricación del día lunes -->  61,000.00

Ganancia de fabricación del día martes -->  89,500.00

Conjuntando todo el modelo matemático anterior obtendríamos la siguiente expresión

Lunes  8 x + 5 y = 61,000
Martes             11 x + 8 y = 89,500

Notamos que obviamente los precios del celular y la computadora son los mismos para los días lunes y martes. Lo único que cambia son las situaciones en las que se ven involucrados los precios, que es el número de productos fabricados.

De modo que para poder conocer el valor del precio de cada producto, es decir, para conocer el valor de x y de y debemos de resolver el sistema de ecuaciones simultaneas.

Antes de empezar, pensemos un momento, si se conociera el precio del celular, ¿se podría calcular fácilmente el precio de la computadora? Al mismo tiempo si se conociera el precio de la computadora, ¿se podría calcular con la misma facilidad el precio del celular? La respuesta a las preguntas anteriores es sí.

$61,000 – 8 (precio del celular -valor conocido-) = 5 (precio de la computadora)

O bien,

$61,000 – 5 (precio de la computadora  -valor conocido-) = 8 (precio del celular)

En otras palabras si se encontrara el valor de x, se podrá calcular fácilmente el valor de y, o de igual manera, si se encontrara el valor de y, se podrá calcular fácilmente el valor de x. Entendemos que para poder resolver el sistema de ecuaciones simultaneas se debe de hallar el valor correcto para x y para y; por lo tanto para resolver el sistema de ecuaciones simultaneas de dos incógnitas, debemos empezar por hallar el valor de una de las dos incógnitas.

Para hallar primeramente el valor de una de las dos incógnitas presentamos los siguientes métodos.

• Método de sustitución.
• Método de igualación.
• Método de reducción.

 

En donde el nombre de cada uno se debe al procedimiento particular que se realiza en el sistema de ecuaciones simultáneas para conocer el valor de una de las incógnitas.

De manera general, el proceso de los tres métodos anteriores consiste en eliminar una de las dos incógnitas en el sistema y así solamente tener una expresión con una sola incógnita. De esta manera el problema se reduce a la solución de una ecuación de primer grado.

A continuación se explica en qué consiste cada método:

1.- Método de Sustitución

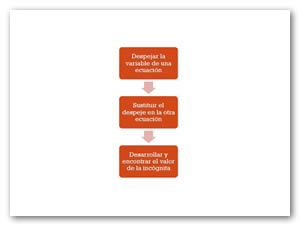
En este método el procedimiento particular para anular una de las dos incógnitas es el sustituir el valor de dicha incógnita según la primera ecuación, en la segunda ecuación. De esta manera la expresión resultante tendrá solo una incógnita, ya que según una de las dos ecuaciones, el valor de una incógnita estará en función de la otra incógnita, de este modo al realizar la sustitución, se obtendrá una sola ecuación con una sola incógnita.

El proceso es el siguiente:

[Aquí va el diagrama de flujo del proceso del Método_de_sustitución.jpg]

De esta manera, al aplicar el método al ejemplo establecido anteriormente se realiza el siguiente proceso:

 

8 x + 5 y = 61,000
11 x + 8 y = 89,500

• Tomamos una de las dos ecuaciones y despejamos a una incógnita

 

[Aquí va la imagen Sustitución_i1.jpg]

Observamos que tras este paso, el valor de y está en función del valor de x.

• Posteriormente el valor del despeje hecho para y, se sustituye en el valor de y de la segunda ecuación

 

De esta manera observamos que en este punto del proceso obtenemos una ecuación de primer grado, pues solamente se tiene una incógnita a encontrar.

• Por último se desarrolla correctamente la ecuación de primer grado para encontrar el valor de su única incógnita

 

Al haber encontrado el valor de una de las dos incógnitas se puede encontrar el valor de la otra. Recordamos que iniciamos con un despeje para encontrar el valor de y, y que este estaba en función de x, es decir conociendo el valor de x se conocerá el valor de y. Por lo que solamente sustituimos el resultado calculado en el despeje inicial para encontrar el valor de y.

De esta manera se hallan los valores de dichas incógnitas en cuestión, y según el razonamiento anterior, el precio de los celulares en la empresa es de $4,500.00, y el precio de las computadoras es de $5,000.00. Resultados que serán corroborados por los otros métodos.

2.- Método de igualación

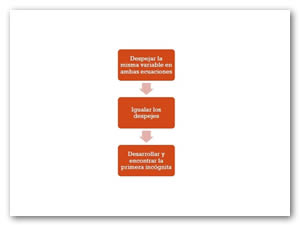
El procedimiento particular de este método para anular una de las dos incógnitas consiste en despejar en ambas ecuaciones la misma variable, apoyándonos del enunciado lógico que dicta que el valor que tenga la y en la primera ecuación es el mismo que tiene en la segunda ecuación; y posteriormente bajo este enunciado, establecer una igualdad entre los dos despejes hechos.

El proceso de este método se muestra a continuación:

Describiendo el anterior proceso de la siguiente manera:

• Tomando, ahora, las dos ecuaciones, realizar en ambas el despeje de la misma incógnita

 

 

• Una vez hecho lo anterior, podemos establecer una igualación entre ambos despejes, ya que ambos son iguales al valor de la incógnita y.

 

 

Notamos nuevamente que después de realizar este paso obtenemos una ecuación en donde solamente se tiene una incógnita.

• Enseguida se desarrolla la ecuación obtenida para hallar el valor de la única incógnita.

 

 

Nuevamente, este método nos ha servido para hallar el valor de una de las incógnitas. Por lo que para encontrar la segunda incógnita nos podemos valer del procedimiento del método anterior. Al inicio establecimos los dos despejes para encontrar el valor de y a partir de conocer el valor de x, es decir:

Observamos la coincidencia en los resultados con el método anterior. Deduciendo nuevamente como respuesta que el precio de los celulares en la empresa es de $4,500.00 y el precio de las computadoras es de $5,000.00.

3.- Método de reducción

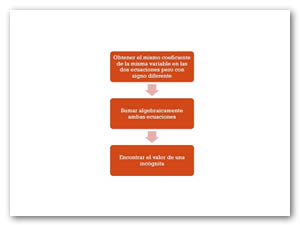
Este es el tercer método que resuelve un sistema de ecuaciones simultáneas cancelando o anulando una de las dos incógnitas y quedándose conociendo el valor de la otra incógnita; su procedimiento consiste en la reducción de las dos ecuaciones en una sola ecuación, a través de la suma algebraica de las mismas. Para esto obviamente, al hacer la suma algebraica de las dos ecuaciones y esperando que se elimine el valor de una de las incógnitas, el término donde se encuentre la variable que se desea eliminar, debe tener en las dos ecuaciones un coeficiente igual, pero en cada ecuación, debe tener signo distinto.

Es evidente que si al inicio no se tiene el coeficiente igual ni el signo diferente del término que contenga a la variable que se desea eliminar en las dos ecuaciones, se deberá hacer una modificación a una o en su caso a ambas ecuaciones. La modificación que se debe hacer no deberá transformar ni alterar el valor ni la proporción de variables y resultado en ninguna de las ecuaciones. Por lo cual la transformación que se hará a una o a las dos ecuaciones será convertirlas en una de sus infinitas ecuaciones equivalentes.

Se llama ecuación equivalente a aquella ecuación que se obtiene a partir de la otra. (Baldor, 2009). Es decir, para encontrar la ecuación equivalente de cualquier ecuación, se debe multiplicar a esta por cualquier cantidad constante.

Por ejemplo:

8 x + 5 y = 61,000  --> Ecuación original

(2)(8 x + 5 y = 61,000) = 16 x + 10 y = 122,000 --> Ecuación equivalente a la original.

Pero ¿cuál es la constante por la que se debe de multiplicar cada ecuación? La respuesta es simple, se debe de multiplicar por el coeficiente que tenga en la otra ecuación, la variable que se desea eliminar. Y posteriormente atribuirle a cada coeficiente un signo que permita que sus resultados tengan signos distintos en los términos de la variable que se eliminará.

El procedimiento es el siguiente:

Es decir, supongamos que se desea eliminar la incógnita y,

(8)(8 x + 5 y = 61,000)    -->      64 x + 40 y =  488,000
(-5)(11 x + 8 y = 89,500)  -->  - 55 x – 40 y = -447,500

 

Posteriormente se realizará la suma algebraica de ambas ecuaciones para obtener nuevamente una sola ecuación con una incógnita.

Por lo que únicamente se despeja la incógnita para hallar su valor.

Una vez más se demuestra el procedimiento para eliminar una incógnita y poder conocer el valor de la otra. Por lo que solamente resta sustituir dicho valor y encontrar la segunda incógnita como en los métodos anteriores, pero de igual manera, debido a que es un procedimiento igual de rápido que sencillo, podemos utilizar ese mismo método para encontrar el valor de la incógnita y, a partir de la eliminación de la variable x.

(11)(8 x + 5 y = 61,000)  -->   88 x + 55 y =  671,000
(- 8)(11 x + 8 y = 89,500)  -->  - 88 x – 64 y = -716,000

 

De esta manera se verifica el resultado que permite concluir lo mismo que en al utilizar los métodos anteriores.

Como podemos darnos cuenta si se trata al sistema por separado, cada una de las dos ecuaciones pueden tener una infinidad de soluciones que le hacen que se cumpla el resultado condicionante, pero visto como un sistema simultaneo, se debe de hallar solo el valor que cumpla con las condiciones para las dos ecuaciones, es decir un valor que represente una intersección entre el conjunto soluciones de la primera ecuación con el conjunto de las soluciones de la segunda. Es por ello que, además de los métodos de eliminación de una de las dos incógnitas, analizaremos un método que ejemplifica la afirmación inicial en el párrafo, dicho método es el siguiente:

4.- Método Gráfico

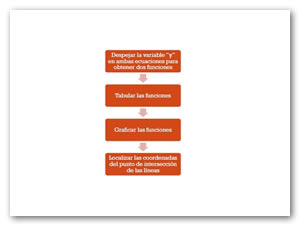
El método gráfico consiste en hallar la intersección de los conjuntos solución de ambas ecuaciones, que no es otra cosa que la representación de un punto de intersección en una gráfica, para ello debemos representar claramente en un gráfico los conjuntos solución de ambas ecuaciones, lo cual se puede hacer cuando se pone una incógnita en función de la otra, es decir, por ejemplo, despejar a la incógnita y nuevamente en ambas ecuaciones, ya que de esta manera se establece que el valor de y está en función de los valores que pueda tomar la incógnita x, siendo así y la variable dependiente y x la variable independiente. En donde la variable independiente puede tomar arbitrariamente cualquier valor de los números reales, arrojando así para y un valor determinado.

Por definición, una función es una correspondencia que asigna a cada elemento x de un conjunto, exactamente un elemento y de otro conjunto. (Swokowski & Cole, 2011)

Este método tiene el siguiente proceso:

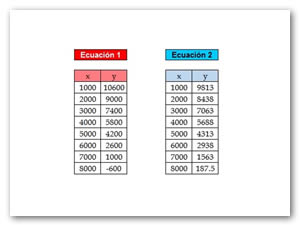
En otras palabras, después de despejar la misma incógnita en las dos ecuaciones, se realiza una tabulación de los dos despejes para encontrar algunos de los valores que representan el conjunto solución en ambas ecuaciones, los cuales en la gráfica representarán líneas rectas.

Aplicándolo al ejemplo obtenemos lo siguiente:

• De ambas ecuaciones despejamos a la misma incógnita

 

 

• Se tabulan las funciones obtenidas asignando a la variable independiente valores arbitrarios

Posteriormente se grafican las dos tabulaciones, sabiendo que cada uno de los valores de las tabulaciones para x y y representarán las coordenadas de un punto en la gráfica, obtendremos así en la gráfica una línea recta que corresponderá a cada una de las funciones.

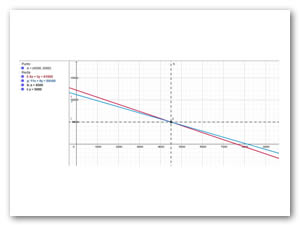
Interpretando la gráfica, observamos que toda la primera línea representa el conjunto de soluciones que satisfacen solo a la primera ecuación, mientras que de igual manera la segunda línea representa el conjunto de soluciones que solo satisfacen a la segunda ecuación, por lo tanto el punto de intersección de las líneas es aquel punto que representa la solución correcta, ya que satisface tanto la primera ecuación como al mismo tiempo la segunda. Los valores para cada una de las incógnitas se encuentran en las coordenadas del punto de intersección de ambas líneas.

Como se puede apreciar en la gráfica, las líneas convergen en un punto cuyas coordenadas son 4500 para x y 5000 para y. De esta manera comprobamos nuevamente que los resultados en este método coinciden con todos los demás.

Sin embargo

Independientemente del método de solución elegido, es importante realizar la comprobación de los resultados obtenidos sustituyendo los resultados en sus respectivos valores para x y para y, y si al término del desarrollo el valor numérico de la ecuación coincide con la condición de igualdad podemos decir que hemos encontrado la solución correcta ya que satisface a ambas ecuaciones.

Bibliografía

Baldor, A. (2009). Álgebra. México: Grupo Editorial Patria.

Swokowski, E. W., & Cole, J. A. (2011). Álgebra y Trigonometría con Geometría Analítica. México, D. F.: Cengage Learning.

 

^[a] Escuela Preparatoria Número 4, Universidad Autónoma del Estado de Hidalgo. pedro_soto@uaeh.edu.mx